Rectas Coplanarias

Se dice que dos o más rectas son coplanarias cuando se encuentran contenidas en un mismo plano.

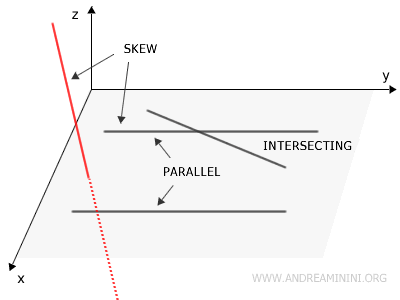
En otras palabras, dos o más rectas son coplanarias si existe al menos un plano único que las incluya a todas.

Las rectas coplanarias pueden clasificarse en:

• Rectas secantes
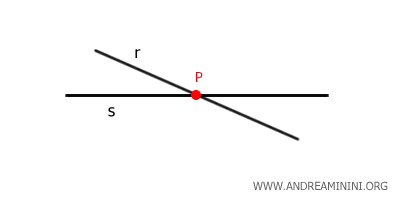
  Dos rectas en un plano son secantes si se cortan en un único punto. Desde el punto de vista matemático, esto significa que existe un punto en el espacio (x, y, z) que pertenece simultáneamente a ambas rectas.
  
• Rectas paralelas
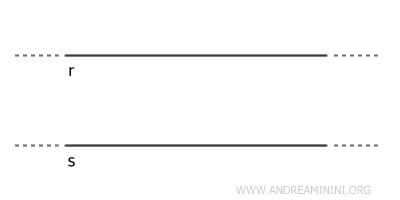
  Dos o más rectas en un plano son paralelas si no se interceptan en ningún punto. Poseen la misma dirección pero nunca se cruzan, y permanecen siempre en el mismo plano.
  
• Rectas coincidentes
  Dos rectas son coincidentes si comparten exactamente todos sus puntos. Dado que una recta está formada por infinitos puntos, las rectas coincidentes tienen todos sus puntos en común. Constituyen un caso particular de rectas paralelas, pues en esencia son la misma recta, aunque puedan representarse mediante ecuaciones diferentes.

Diferencia entre rectas coplanarias y rectas alabeadas. Las rectas coplanarias se diferencian de las rectas alabeadas en que estas últimas ni se intersectan ni son paralelas, y por lo tanto no se hallan en un mismo plano. Las rectas alabeadas son un fenómeno exclusivo del espacio tridimensional y no pueden existir en un plano bidimensional. En cambio, las rectas coplanarias son un concepto fundamental en la geometría euclidiana.

Un Ejemplo Práctico

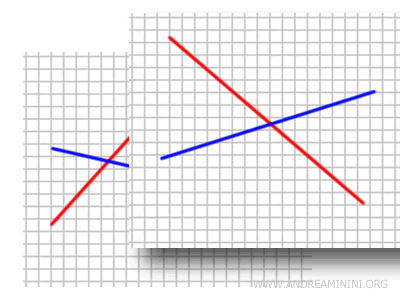
Un ejemplo muy habitual de rectas coplanarias son las rectas dibujadas sobre una hoja de papel.

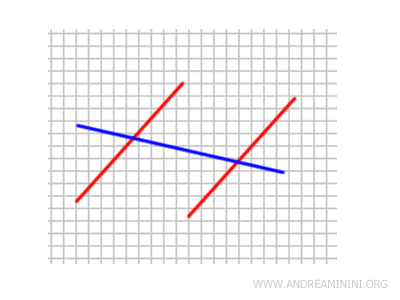
Todas las rectas trazadas sobre la misma hoja son coplanarias, ya que se sitúan en el mismo plano: la superficie del papel. Estas rectas pueden ser paralelas o secantes.

Por el contrario, dos rectas dibujadas en hojas diferentes, aunque estén una sobre otra (por ejemplo, en un cuaderno), no son coplanarias, ya que pertenecen a planos distintos.

Y así sucesivamente.