Ángulos alternos
Si tenemos dos rectas «r» y «s» y una transversal «t», se denominan ángulos alternos aquellos que no comparten vértice y se encuentran a lados opuestos de la transversal.
Los ángulos alternos se dividen en:
- Ángulos alternos interiores
cuando se sitúan en la zona comprendida entre las rectas «r» y «s». - Ángulos alternos exteriores
cuando se encuentran fuera del espacio delimitado por las rectas «r» y «s».
Un ejemplo práctico
Imaginemos dos rectas «r» y «s».
Una transversal «t» corta ambas rectas en puntos distintos.
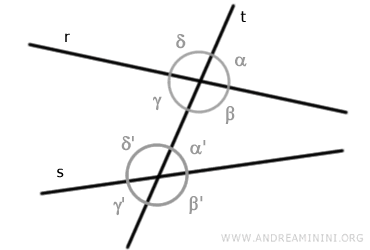
En los puntos de intersección se forman dos pares de ángulos.
Los ángulos (β, δ') que aparecen en rojo son ángulos alternos interiores porque no comparten vértice y se ubican en lados opuestos de la transversal «t».
Se denominan interiores porque están comprendidos entre las rectas «r» y «s».
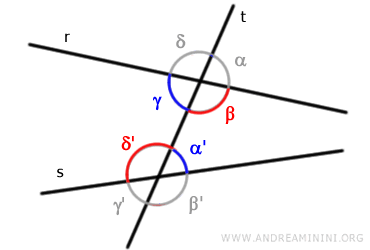
Del mismo modo, los ángulos (γ, α') señalados en azul también son ángulos alternos interiores por las mismas razones.
Por otro lado, los ángulos (α, γ') mostrados en rojo son ángulos alternos exteriores porque no comparten vértice y se sitúan en lados opuestos de la transversal «t».
Se denominan exteriores porque se encuentran fuera del espacio comprendido entre las rectas «r» y «s».
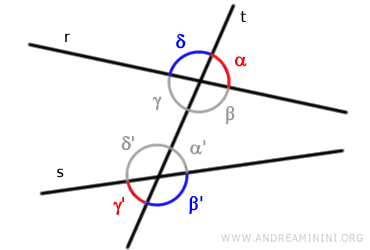
Igualmente, los ángulos (β', δ) señalados en azul son ángulos alternos exteriores por las mismas razones.
Y así sucesivamente.