Ángulos Adyacentes
Los ángulos adyacentes son dos ángulos que comparten el mismo vértice y uno de sus lados, mientras que sus lados no comunes están alineados, es decir, se sitúan sobre una misma recta.
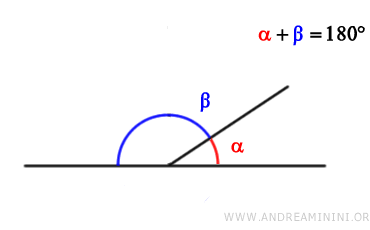
En otras palabras, dos ángulos son adyacentes cuando son ángulos consecutivos cuyos lados no comunes se encuentran sobre la misma línea recta, prolongándose en direcciones opuestas.
La suma de dos ángulos adyacentes es siempre igual a un ángulo llano (180° o π radianes).
Por tanto, los ángulos adyacentes son también ángulos suplementarios, y viceversa.
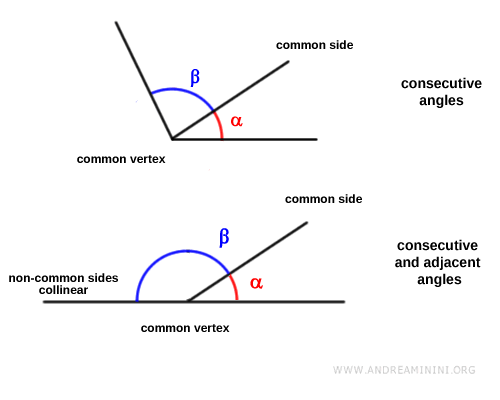
Diferencia entre ángulos adyacentes y ángulos consecutivos. Conviene tener presente que dos ángulos adyacentes son siempre consecutivos. No obstante, lo contrario no siempre es cierto: dos ángulos consecutivos no tienen por qué ser adyacentes. Esto se debe a que la suma de dos ángulos adyacentes es siempre 180°, mientras que la suma de dos ángulos consecutivos puede variar. Tanto los ángulos adyacentes como los consecutivos comparten vértice y un lado. La diferencia esencial de los ángulos adyacentes es que sus lados no comunes están perfectamente alineados. En cambio, en los ángulos consecutivos, estos lados pueden no encontrarse sobre la misma recta.
Un ejemplo práctico
Consideremos dos ángulos:
$$ \alpha = 60° $$
$$ \beta = 120° $$
Ambos ángulos comparten vértice y uno de sus lados. Los otros dos lados se encuentran alineados sobre la misma recta.
Por lo tanto, estos dos ángulos son ángulos adyacentes.
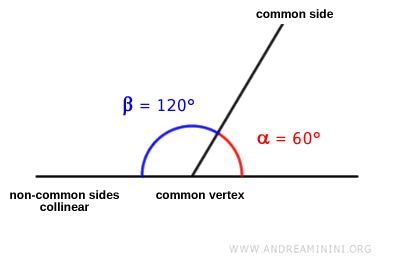
La suma de estos dos ángulos es igual a 180°.
$$ \alpha + \beta = 180° $$
Y así sucesivamente.