Suma de Ángulos
Para sumar dos ángulos consecutivos, basta calcular la medida del ángulo comprendido entre sus lados no comunes. $$ a \hat{O} b + b \hat{O} c = a \hat{O} c $$
Cuando hablamos de sumar ángulos, nos referimos a sumar sus medidas, ya sea en grados o en radianes.
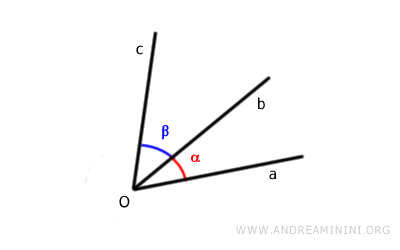
Ejemplo. Consideremos dos ángulos adyacentes, aȮb y bȮc. Sus lados no comunes son a y c.
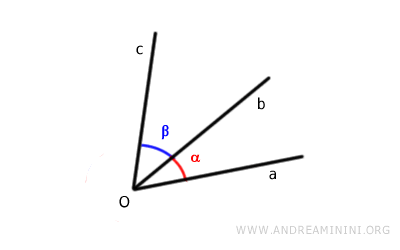
Para determinar la suma de los ángulos, se mide el ángulo formado entre los lados no comunes, es decir, aȮc.
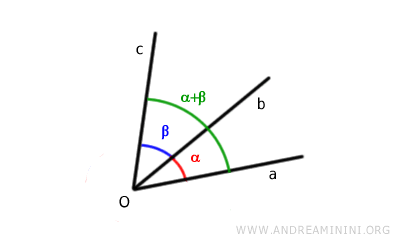
¿Cómo se suman ángulos que no son adyacentes?
Geométricamente, la regla de la suma de ángulos adyacentes también puede aplicarse a ángulos que no lo son.
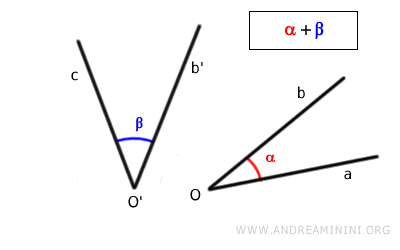
Por ejemplo, consideremos dos ángulos no adyacentes.
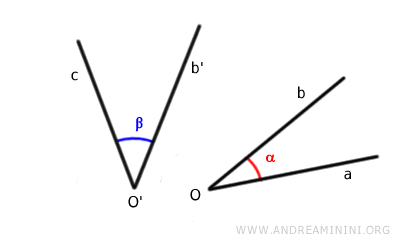
Se hace coincidir el vértice del primer ángulo con el vértice del segundo.
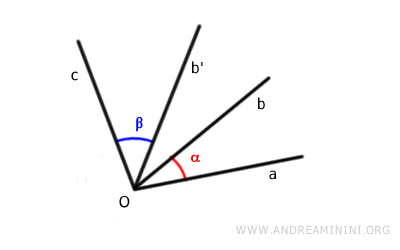
Mediante un movimiento rígido, se hace coincidir uno de los lados del primer ángulo con uno de los lados del segundo.
De este modo, los dos ángulos quedan adyacentes y conservan la congruencia con respecto a los ángulos originales.
Así, puede aplicarse la misma regla que para los ángulos adyacentes: basta medir el ángulo comprendido entre los lados no comunes.
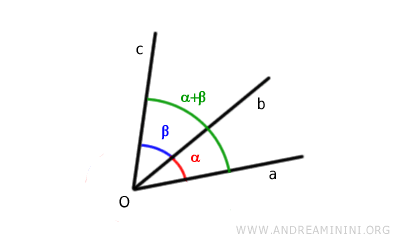
Nota. Desde un punto de vista matemático, basta con medir los ángulos α y β con un transportador y sumar sus valores (α+β), sin importar si los ángulos son adyacentes o no.
Propiedades de la Suma de Ángulos
Algunas propiedades relevantes de la suma de ángulos:
- Si se tienen dos pares de ángulos congruentes, α≅β y γ≅δ, sus sumas también son congruentes, es decir, tienen la misma medida. $$ \alpha \cong \beta \ , \ \gamma \cong \delta \ , \ \Longrightarrow \alpha + \gamma \cong \beta + \delta $$
- Si se consideran cuatro ángulos agrupados en dos pares no congruentes, y se cumple que α>β y γ>δ, entonces sus sumas tampoco serán congruentes y mantendrán el mismo orden de desigualdad. $$ \alpha > \beta \ , \ \gamma > \delta \ , \ \Longrightarrow \alpha + \gamma > \beta + \delta $$
Y así sucesivamente.