Ángulo orientado

¿Qué es un ángulo orientado?

Un ángulo orientado es aquel formado entre dos lados y definido por un sentido de giro.

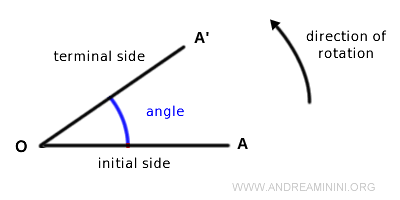
En un ángulo orientado, el orden de los lados es fundamental. El primer lado se llama lado inicial y el lado que se alcanza tras girar se denomina lado final.

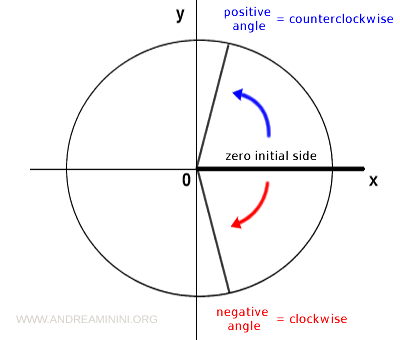
Por convención, un ángulo se considera positivo si el giro es en sentido antihorario, y negativo si es en sentido horario.

El lado inicial cero suele coincidir con el eje x positivo del plano cartesiano.

Nota: Para representar un ángulo α menor que una vuelta completa y todos los infinitos ángulos orientados que se obtienen sumando vueltas enteras, se emplea la notación en grados $$ \alpha + k \cdot 360° \ \ \ con \ k \in \mathbb{Z} $$ o en radianes $$ \alpha + k \cdot 2 \pi \ \ \ con \ k \in \mathbb{Z} $$. Por ejemplo, para expresar el ángulo α = 800°, se toma k = 2 y se escribe $$ \alpha = 80° + 360 \cdot 2 $$

Un ejemplo práctico

Veamos un ejemplo de ángulo orientado.

$$ a \hat{O} b $$

El lado inicial es el lado “a”, mientras que el lado final es el lado “b”. El vértice se sitúa en el punto O.

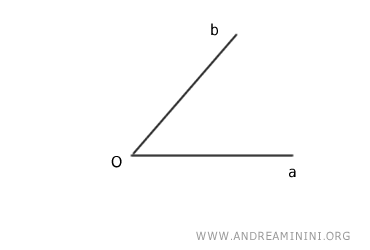
¿Cuál es la medida de este ángulo orientado?

Al tratarse de un ángulo orientado, todavía no podemos determinar su medida porque no hemos especificado el sentido de giro.

Existen dos posibilidades:

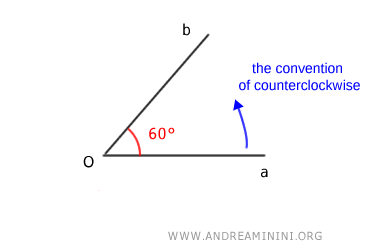
Si el ángulo se mide en sentido antihorario, su medida es de 60°.

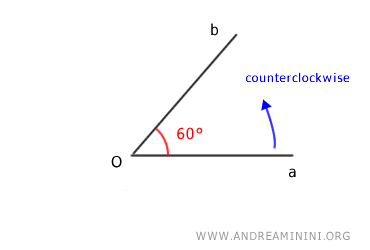
Por el contrario, si se mide en sentido horario, su medida es de 300°.

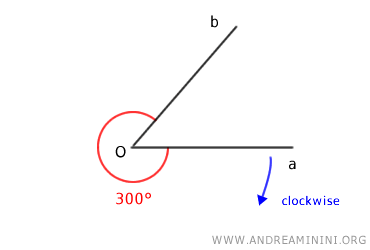
En ambos casos, el lado “a” es el lado inicial, pero la medida resulta completamente distinta.

Así, la medida de un ángulo orientado depende exclusivamente del sentido de giro que se adopte.

Nota: Para evitar confusiones, cuando no se indica el sentido en un ángulo orientado, se adopta por convención el sentido antihorario. Por tanto, en este ejemplo, el ángulo orientado se considera de 60°.

Ángulos positivos y negativos

El signo positivo o negativo de un ángulo orientado depende del movimiento del segmento OA y del sentido de giro que se haya establecido como referencia.

• Si se adopta el sentido antihorario como referencia, el ángulo orientado es positivo si gira en ese mismo sentido, y negativo si gira en sentido horario.
  

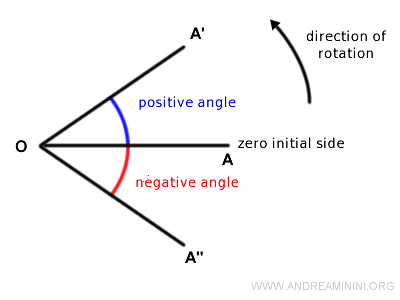
  Nota: En este caso, la rotación del segmento de OA hacia OA' coincide con el sentido de referencia, por lo que el ángulo es positivo. En cambio, la rotación de OA hacia OA" es contraria, y el ángulo se considera negativo.

• Si se adopta el sentido horario como referencia, el ángulo orientado es positivo si gira en ese sentido, y negativo si gira en sentido antihorario.
  

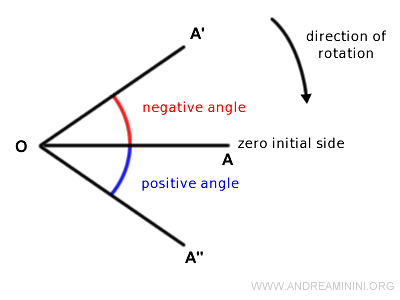
  Nota: En este caso, la rotación del segmento de OA hacia OA" sigue el sentido de referencia y el ángulo es positivo. En cambio, la rotación de OA hacia OA' es opuesta, y el ángulo resulta negativo.

¿Qué ocurre si no se define un sentido de giro como referencia?

Si no se especifica el sentido de giro como sistema de referencia, en matemáticas y física se adopta, por convención, el sentido antihorario, tomando como lado inicial el eje x positivo.

Así, un ángulo orientado será positivo si el segmento gira en sentido antihorario, y negativo si gira en sentido horario.

¿Para qué sirven los ángulos orientados?

En muchos casos, conocer únicamente la medida de un ángulo no basta para disponer de toda la información necesaria.

Por ejemplo, imagina que necesito girar el timón 30°. Pero ¿hacia dónde? ¿Hacia la derecha o hacia la izquierda?

 

Para poder interpretarlo, primero debo establecer un sentido de giro como sistema de referencia.

Supongamos que adopto el sentido antihorario.

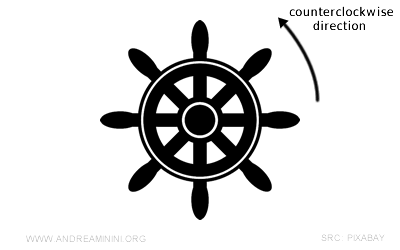
Así puedo comprender correctamente la dirección del giro.

Como 30° es positivo, significa que el giro sigue el mismo sentido de referencia.

Por tanto, debo girar el timón en sentido antihorario, es decir, hacia la izquierda.

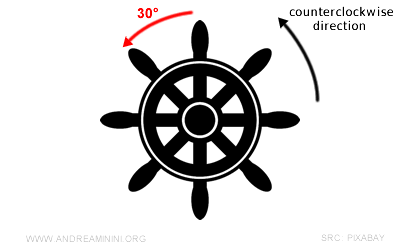
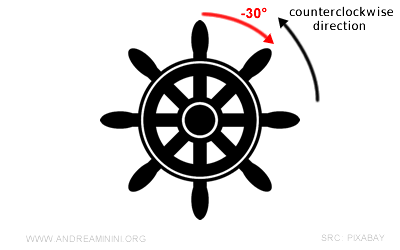
Si el ángulo orientado hubiera sido de -30°, tendría que girar el timón hacia la derecha, pues sería contrario al sentido de referencia.

Características de los ángulos orientados

Los ángulos orientados presentan dos características esenciales:

• Los ángulos orientados pueden tener medida negativa
  Un ángulo es negativo cuando su giro se opone al sentido de referencia adoptado. Por ejemplo, un ángulo de -20°.
  
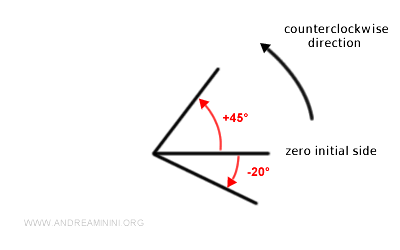
• Los ángulos orientados pueden superar una vuelta completa de 360° (2π radianes)
  Por ejemplo, un ángulo orientado de 730° indica que debemos realizar dos vueltas completas en el sentido de referencia y sumar 10° más.
  
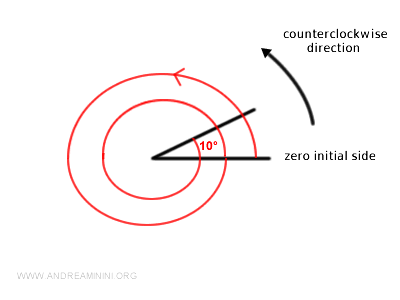
  Desde el punto de vista algebraico: $$ 730° = 360° \cdot 2 + 10° $$ $$ 730° = 720° + 10° $$

Notación simplificada de ángulos orientados

Un ángulo orientado mayor a 360° puede expresarse de forma simplificada como la suma de un ángulo menor a 360° y un número entero de vueltas completas, es decir: $$ \alpha° + 360° \cdot k $$ Si el ángulo se expresa en radianes, se utiliza 2π: $$ \alpha + 2 \pi \cdot k $$ En ambos casos, k es un número entero.

Si no se indica k, la notación representa todos los ángulos orientados que difieren en un múltiplo entero de la vuelta completa.

Donde k es un número entero, positivo o negativo.

Ejemplo 1

Un ángulo orientado de 730° puede expresarse como:

$$ 730° = 360° \cdot 2 + 10° $$

siendo k = 2.

Ejemplo 2

Si no se especifica el valor de k:

$$ \frac{ \pi }{ 2 } + k \cdot 2 \pi $$

la notación representa todos los ángulos de 90° (o π/2) que difieren en múltiplos de una vuelta completa (2π):

$$ \frac{ \pi }{ 2 } + k \cdot 2 \pi = \{ \frac{ \pi }{ 2 }, \ \frac{ \pi }{ 2 } \pm 2 \pi, \ \frac{ \pi }{ 2 } \pm 4 \pi, \ \ldots \} $$

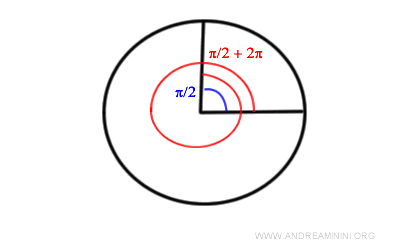
En la siguiente figura se muestra una representación gráfica de π/2 (en azul) y π/2 + 2π (en rojo).

En el primer caso, k = 0; en el segundo, k = 1.

Y así sucesivamente.