Suma o Resta de Ángulos Congruentes
Si dos ángulos se obtienen sumando (o restando) pares de ángulos congruentes situados en posiciones correspondientes, entonces los ángulos resultantes también serán congruentes.
En otras palabras, si tenemos dos pares de ángulos congruentes:
$$ \alpha \cong \beta $$
$$ \gamma \cong \delta $$
entonces la suma de los ángulos correspondientes también será congruente:
$$ \alpha + \gamma \cong \beta + \delta $$
Lo mismo ocurre con la diferencia:
$$ |\alpha - \gamma| \cong |\beta - \delta| $$
Esto se debe a que la congruencia se mantiene al operar con ángulos de igual medida:
Nota. Dos ángulos son congruentes cuando tienen la misma medida, es decir, cuando coinciden perfectamente al superponerse, sin importar su posición en el plano.
Ejemplos Prácticos
Supongamos que tenemos dos pares de ángulos congruentes: $ \alpha \cong \beta = 45° $ y $ \gamma \cong \delta = 30° $.
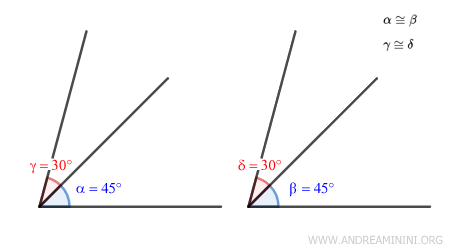
La suma de los ángulos α + γ y β + δ es idéntica: 75°.
$$ \alpha + \gamma = 45° + 30° = 75° $$
$$ \beta + \delta = 45° + 30° = 75° $$
Del mismo modo, al restar, tanto α - γ como β - δ dan como resultado 15°.
$$ \alpha - \gamma = 45° - 30° = 15° $$
$$ \beta - \delta = 45° - 30° = 15° $$
Por lo tanto, ya sea que sumemos o restemos pares de ángulos congruentes, el resultado seguirá siendo congruente.
Nota. Esta propiedad es especialmente útil en geometría, sobre todo cuando se trabaja con ángulos obtenidos mediante construcciones o transformaciones geométricas. Además, permite tratar las expresiones angulares de manera algebraica, centrándose en sus medidas más que en su posición en el plano.
Demostración
Partamos de dos pares de ángulos congruentes:
$$ \alpha \cong \beta $$
$$ \gamma \cong \delta $$
Consideremos ahora las sumas de los pares no congruentes:
$$ \alpha + \gamma $$
$$ \beta + \delta $$
Como $ \gamma \cong \delta $, podemos sustituir uno por otro en la expresión $ \alpha + \gamma $:
$$ \alpha + \gamma = \alpha + \delta $$
Y dado que $ \alpha \cong \beta $, podemos aplicar la misma sustitución en $ \alpha + \delta $:
$$ \alpha + \gamma = \alpha + \delta = \beta + \delta $$
De este modo, ambas sumas tienen la misma medida:
$$ \alpha + \gamma \cong \beta + \delta $$
Por lo tanto, son congruentes.
Nota. El mismo razonamiento se aplica a la resta: $$ \alpha - \gamma $$ $$ \beta - \delta $$ Dado que $ \gamma \cong \delta $, podemos escribir: $$ \alpha - \gamma = \alpha - \delta $$ Y como $ \alpha \cong \beta $, se obtiene: $$ \alpha - \gamma = \alpha - \delta = \beta - \delta $$ Por lo tanto, ambas diferencias también tienen la misma medida: $$ \alpha - \gamma \cong \beta - \delta $$
Esto demuestra que la suma (o la diferencia) de ángulos congruentes produce ángulos que siguen siendo congruentes.
Y así sucesivamente.