Lados Correspondientes y Opuestos de un Ángulo

En dos ángulos cuyos lados son paralelos, se denomina:

• Lados correspondientes
  a aquellos que se sitúan en el mismo lado respecto a la recta que une los vértices de ambos ángulos.
• Lados opuestos
  a aquellos que se encuentran en lados opuestos respecto a la recta que une los vértices de los dos ángulos.

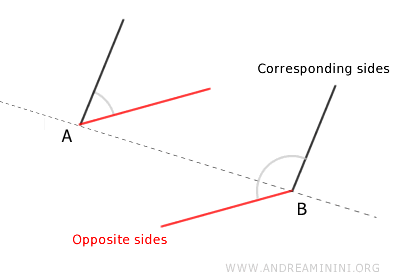
Si los lados paralelos de dos ángulos son todos correspondientes o todos opuestos, entonces los ángulos son congruentes. En caso contrario, los ángulos son suplementarios, es decir, la suma de sus medidas es 180°.

Explicación

Partimos de dos ángulos cuyos lados son paralelos.

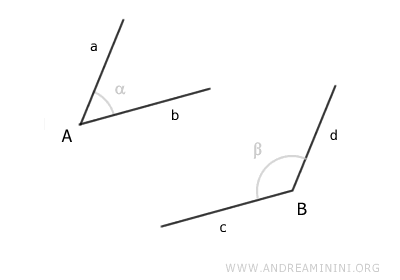
Se traza una recta r que pasa por los vértices A y B de ambos ángulos.

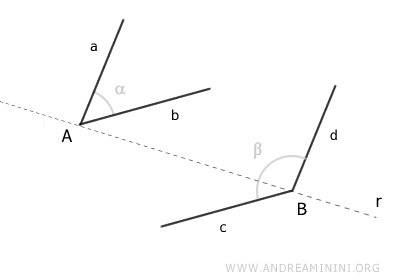
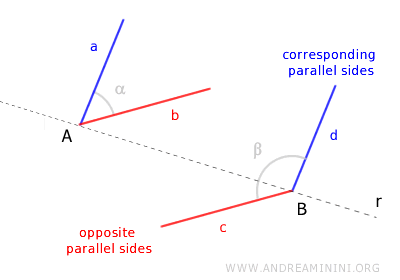
Si los lados paralelos de estos ángulos se encuentran todos en el mismo lado (ya sea a la izquierda o a la derecha) respecto a la recta r, se denominan “lados correspondientes”.

En este caso, los lados paralelos correspondientes son los lados a y d.

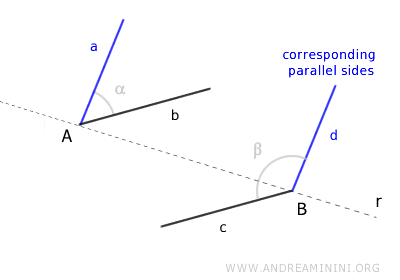
Si, por el contrario, un lado está a la izquierda y el otro a la derecha de la recta r, estos lados paralelos se llaman “lados opuestos”.

En este caso, los lados paralelos opuestos son los lados b y c.

Observaciones

Algunas observaciones útiles sobre los lados correspondientes y opuestos de un ángulo:

• Dos ángulos con lados paralelos son congruentes si todos sus lados paralelos son o bien correspondientes o bien opuestos.

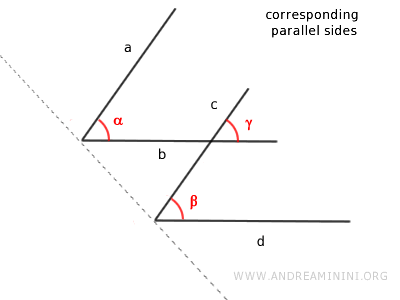
  Demostración (lados correspondientes). Estos ángulos tienen lados paralelos a||c y b||d. Los ángulos β y γ son ángulos correspondientes de dos rectas paralelas b y d, cortadas por la recta c. Por lo tanto, según el teorema de las rectas paralelas, son ángulos congruentes β≅γ. Del mismo modo, los ángulos α y γ son ángulos correspondientes de las rectas paralelas a y c cortadas por la recta b, por lo que también son congruentes α≅γ. Finalmente, aplicando la propiedad transitiva, si α≅γ y β≅γ, entonces los ángulos α y β también son congruentes α≅β.
  
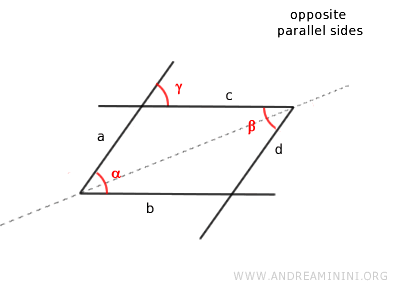
  Demostración (lados opuestos). Estos ángulos tienen lados paralelos a||d y b||c. Los ángulos β y γ son ángulos alternos internos formados por dos rectas paralelas a y d cortadas por la recta c. Según el teorema de las rectas paralelas, son congruentes β≅γ. Los ángulos α y γ son ángulos correspondientes de las rectas paralelas c y b cortadas por la recta a, por lo que también son congruentes α≅γ. Finalmente, aplicando la propiedad transitiva, si α≅γ y β≅γ, entonces los ángulos α y β son también congruentes α≅β.
  

• Dos ángulos con lados paralelos son suplementarios si poseen dos lados correspondientes y dos lados opuestos.
  

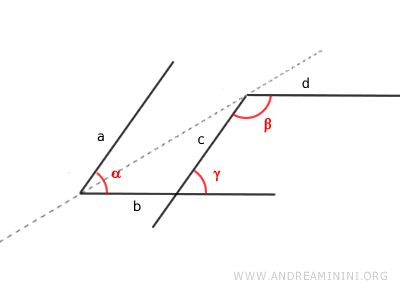
  Demostración. Estos ángulos tienen dos lados paralelos opuestos a||c y dos lados paralelos correspondientes b||d. Los ángulos β y γ son ángulos consecutivos internos formados por dos rectas paralelas b y d cortadas por la recta c. Según el teorema de las rectas paralelas, estos ángulos son suplementarios β+γ=180°. Por su parte, los ángulos α y γ son ángulos correspondientes de las rectas paralelas a y c cortadas por la recta b, por lo que son congruentes α≅γ. Finalmente, por la propiedad transitiva, si α≅γ y β+γ=180°, entonces los ángulos α y β también son suplementarios α+β=180°.
  

Y así sucesivamente.