Postulado de Divisibilidad de Ángulos
Todo ángulo α con medida distinta de cero puede dividirse en n > 0 partes congruentes.
Donde n es cualquier número natural.
La enésima parte de dicho ángulo es un submúltiplo β del propio ángulo.
$$ \beta = \frac{1}{n} \alpha $$
Un Ejemplo Práctico
Consideremos un ángulo α que mide 45°.
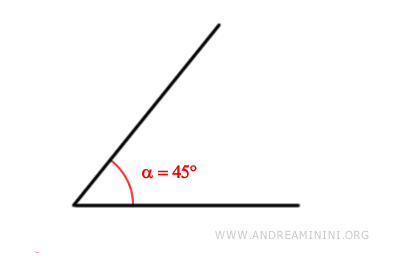
Dividimos este ángulo en n = 3 partes iguales.
$$ \beta = \frac{1}{3} \cdot 45° = 15° $$
Cada parte es un ángulo β de 15°, que constituye un submúltiplo del ángulo original α.
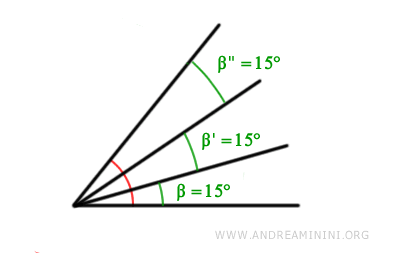
La suma de los tres ángulos de 15° nos devuelve exactamente el ángulo original α (45°).
$$ 15° + 15° + 15° = 45° $$
Del mismo modo, podemos dividir el ángulo α en tantas partes como se desee.
Y así sucesivamente.