Axioma de Transporte de Ángulos
Dada una semirrecta con origen en O' y un ángulo aOb con vértice en O, definido con un sentido de giro determinado, existe un único ángulo cO'd en el semiplano tal que los ángulos aOb y cO'd son congruentes entre sí. $$ aOb \ \cong \ cO'd $$
El axioma de transporte de ángulos es un principio fundamental en la geometría euclidiana, ya que establece una propiedad esencial de los ángulos.
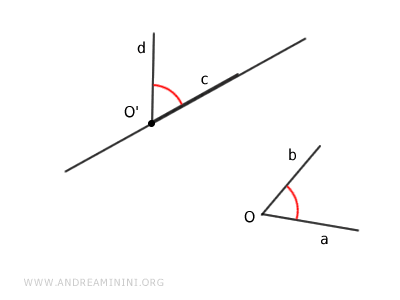
En esencia, el axioma indica que es posible trasladar o “copiar” un ángulo de un lugar a otro conservando su medida.
Por ejemplo, si tomo un ángulo y lo desplazo mediante un movimiento rígido (como una rotación, una traslación, etc.) sin modificar su amplitud, el nuevo ángulo formado es congruente con el original.
Nota: Este axioma se deriva del más amplio “Postulado de las Transformaciones Rígidas” o “Postulado de Euclides”, que establece que pueden realizarse traslaciones, rotaciones y simetrías en el espacio sin alterar la medida de los ángulos.
Y así sucesivamente.