Ángulos cóncavos y convexos
En geometría, los ángulos pueden clasificarse según distintas características, entre ellas si se trata de ángulos cóncavos o convexos.
Nota: La diferencia entre ángulos cóncavos y convexos se basa en la disposición de los puntos dentro del ángulo en relación con sus lados o con las prolongaciones de estos.
Ángulos cóncavos
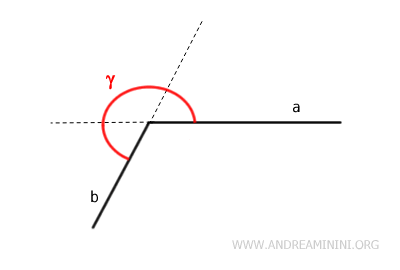
Un ángulo cóncavo es aquel que abarca también las prolongaciones de sus lados dentro de su amplitud.
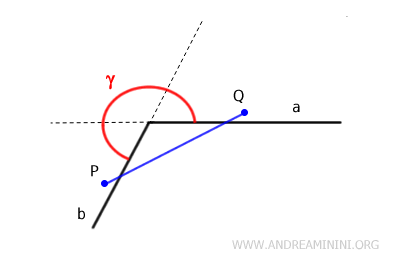
En cualquier ángulo cóncavo, siempre existe al menos un par de puntos, P y Q, ubicados en su interior, de forma que, al trazar el segmento PQ que los une, una parte de dicho segmento queda fuera del ángulo. Es decir, atraviesa puntos exteriores al ángulo.
Se puede considerar un ángulo cóncavo como aquel cuyas lados se “abren” hacia fuera, superando los 180° de amplitud.
Nota: Es importante destacar que un ángulo completo, es decir, de 360 grados, no se clasifica como ángulo cóncavo. Esto se debe a que cualquier segmento trazado entre dos puntos situados en su interior queda siempre contenido por completo dentro del ángulo. Por tanto, un ángulo cóncavo mide más de 180° pero menos de 360°.
Ángulos convexos
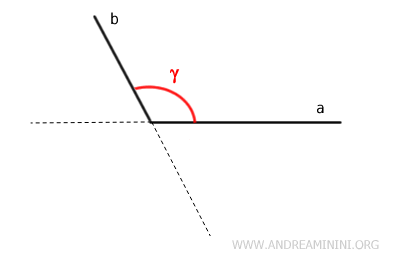
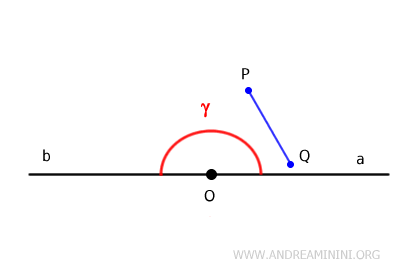
Se denomina ángulo convexo a aquel que no incluye las prolongaciones de sus lados dentro de su extensión.
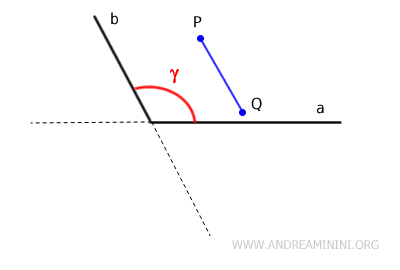
En este caso, si se elige cualquier par de puntos P y Q ubicados dentro del ángulo y se traza el segmento que los une, dicho segmento PQ permanece completamente contenido en el interior del ángulo.
En otras palabras, el segmento no atraviesa ningún punto exterior al ángulo.
Los ángulos convexos pueden interpretarse como ángulos que “cierran” su abertura sobre sí mismos, con una amplitud comprendida entre 0 y 180°.
Nota: Esto incluye el ángulo llano, es decir, el ángulo de 180 grados. Aunque sus lados están situados sobre una misma línea recta, sigue considerándose convexo, ya que los puntos sobre sus lados no se consideran puntos interiores del ángulo. Así, cualquier segmento trazado entre dos puntos situados dentro del ángulo llano permanece siempre contenido en su interior y no atraviesa puntos externos.
Y así sucesivamente.