Ángulo convexo

Se denomina ángulo convexo a aquel que no abarca las prolongaciones de sus lados dentro de su apertura.

En otras palabras, un ángulo convexo es aquel que “cierra” sobre sí mismo y cuya medida se encuentra entre 0° y 180°.

Se diferencia de otros tipos de ángulos, como los ángulos cóncavos, cuya amplitud supera los 180° pero es menor que 360°.

Dentro de la categoría de ángulos convexos se incluyen los ángulos obtusos (mayores de 90° y menores de 180°), los rectos (exactamente 90°) y los agudos (menores de 90°).

Observaciones

Algunas consideraciones sobre los ángulos convexos:

• En un ángulo convexo, si se eligen dos puntos interiores cualesquiera, P y Q, el segmento PQ que los une queda completamente contenido dentro del ángulo. Esto significa que dicho segmento no corta los lados del ángulo ni atraviesa puntos externos a él.
  
• ¿Se puede considerar convexo un ángulo llano (180°)?
  Si se seleccionan dos puntos interiores cualesquiera, P y Q, el segmento PQ no atraviesa puntos exteriores ni corta los lados del ángulo. Por este motivo, el ángulo llano puede considerarse convexo.
  

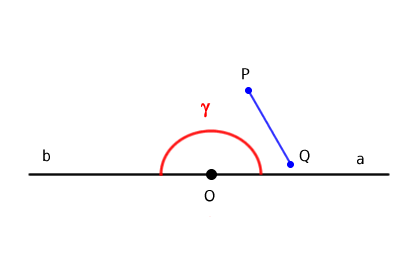
  Explicación: Los puntos que se encuentran sobre los lados “a” y “b” del ángulo γ no se consideran puntos “interiores” del ángulo γ. Por lo tanto, si se toman dos puntos interiores P y Q, el segmento PQ no intersecta los lados ni contiene puntos exteriores al ángulo. En este sentido, el ángulo llano cumple las propiedades de los ángulos convexos.

  No obstante, existen diferentes criterios sobre este asunto. Algunos textos de geometría consideran el ángulo llano como convexo, basándose en los argumentos anteriores. Sin embargo, otros autores lo clasifican como un caso aparte, señalando que “no es menor de 180°” y, por tanto, no puede incluirse estrictamente ni entre los ángulos convexos ni entre los cóncavos.