Hipérbolas con centro en un punto (p,q)
La ecuación de una hipérbola con centro en un punto \((p, q)\) se obtiene a partir de la hipérbola canónica, originalmente centrada en el origen \((0, 0)\), mediante un desplazamiento de coordenadas.
- Hipérbola con eje transverso paralelo al eje \(x\):
La ecuación estándar de una hipérbola centrada en el origen, con eje transverso sobre el eje \(x\), es: $$ \frac{x^2}{a^2} - \frac{y^2}{b^2} = 1 $$ Al trasladar el centro al punto \((p, q)\), la ecuación se transforma en: $$
\frac{(x-p)^2}{a^2} - \frac{(y-q)^2}{b^2} = 1 $$ - Hipérbola con eje transverso paralelo al eje \(y\):
La ecuación estándar de una hipérbola centrada en el origen, con eje transverso sobre el eje \(y\), es: $$
\frac{y^2}{a^2} - \frac{x^2}{b^2} = 1 $$ Al trasladar el centro a \((p, q)\), la ecuación se convierte en: $$
\frac{(y-q)^2}{a^2} - \frac{(x-p)^2}{b^2} = 1 $$
En ambos casos, \(a\) representa la distancia desde el centro hasta los vértices a lo largo del eje transverso, mientras que \(b\) indica la distancia desde el centro hasta los extremos del eje conjugado (también conocido como eje imaginario).
Ecuación general de una hipérbola trasladada
La forma general de una sección cónica viene dada por la ecuación:
$$ Ax^2 + Bxy + Cy^2 + Dx + Ey + F = 0 $$
En esta expresión, \(Ax^2\) y \(Cy^2\) son los términos cuadráticos, \(Bxy\) es el término mixto, y \(Dx\), \(Ey\) son los términos lineales. El valor \(F\) es una constante.
Para obtener esta forma general a partir de la ecuación de una hipérbola centrada en \((p, q)\), como:
$$ \frac{(x-p)^2}{a^2} - \frac{(y-q)^2}{b^2} = 1 $$
procedemos a desarrollar la expresión elevando los binomios al cuadrado:
$$ \frac{(x-p)^2}{a^2} - \frac{(y-q)^2}{b^2} = 1 $$
$$ \frac{x^2 - 2px + p^2}{a^2} - \frac{y^2 - 2qy + q^2}{b^2} = 1 $$
Multiplicamos ambos miembros por \(a^2b^2\) para eliminar los denominadores:
$$ b^2(x^2 - 2px + p^2) - a^2(y^2 - 2qy + q^2) = a^2b^2 $$
Desarrollando y trasladando todos los términos a un solo lado, obtenemos:
$$ b^2x^2 - a^2y^2 - 2b^2px + 2a^2qy + (b^2p^2 - a^2q^2 - a^2b^2) = 0 $$
Al comparar esta expresión con la forma general \(Ax^2 + By^2 + Cx + Dy + E = 0\), identificamos los coeficientes:
- \(A = b^2\)
- \(B = -a^2\)
- \(C = -2b^2p\)
- \(D = 2a^2q\)
- \(E = b^2p^2 - a^2q^2 - a^2b^2\)
Esta forma expandida representa la ecuación de una hipérbola trasladada desde el origen. Cada término refleja un componente específico de la ecuación general de una cónica, en el caso particular de una hipérbola cuyo centro no coincide con el origen.
Un ejemplo práctico
Consideremos ahora un ejemplo concreto de una hipérbola desplazada.
Partimos de la ecuación estándar de una hipérbola con eje transverso horizontal y centrada en el origen \((0, 0)\):
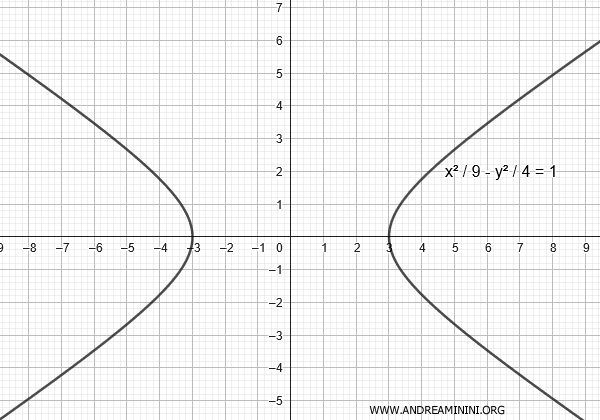
$$ \frac{x^2}{9} - \frac{y^2}{4} = 1 $$
Esta representa una hipérbola horizontal, con \(a^2 = 9\) (es decir, \(a = 3\)) y \(b^2 = 4\) (por lo tanto, \(b = 2\)).
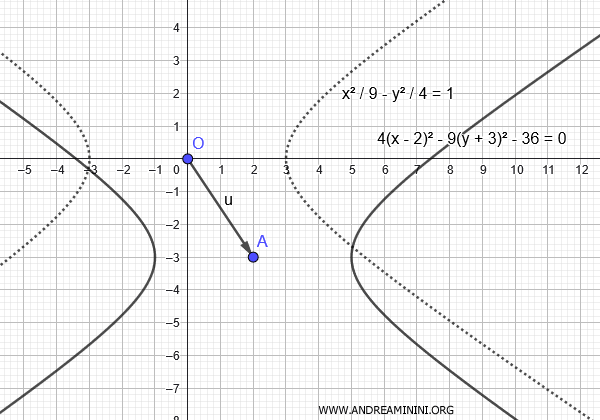
Desplacemos ahora el centro de la hipérbola al punto \((p, q) = (2, -3)\).
La ecuación correspondiente será:
$$ \frac{(x - 2)^2}{9} - \frac{(y + 3)^2}{4} = 1 $$
Desarrollamos esta expresión para obtener su forma general:
$$ \frac{x^2 - 4x + 4}{9} - \frac{y^2 + 6y + 9}{4} = 1 $$
Multiplicamos ambos miembros por 36, el mínimo común múltiplo de 9 y 4, para eliminar los denominadores:
$$ 4(x^2 - 4x + 4) - 9(y^2 + 6y + 9) = 36 $$
Expandiendo los productos:
$$ 4x^2 - 16x + 16 - 9y^2 - 54y - 81 = 36 $$
Reuniendo todos los términos en un solo lado de la ecuación:
$$ 4x^2 - 9y^2 - 16x - 54y + 16 - 81 - 36 = 0 $$
Simplificando los términos constantes:
$$ 4x^2 - 9y^2 - 16x - 54y - 101 = 0 $$
Esta es la ecuación general de la hipérbola cuyo centro ha sido desplazado a \((2, -3)\), conservando los valores originales de \(a^2\) y \(b^2\).
Cálculo de las coordenadas del centro de una hipérbola
Las coordenadas del centro de una hipérbola cuyo centro no está en el origen, y cuya ecuación general es $$ Ax^2 + By^2 + Cx + Dy + E = 0 $$, se determinan mediante la fórmula: $$ \left(p, q\right) = \left(-\frac{C}{2A}, - \frac{D}{2B}\right) $$
Ejemplo
Consideremos la siguiente ecuación general de una hipérbola desplazada:
$$ 4x^2 - 9y^2 - 16x - 54y - 101 = 0 $$
En este caso, los coeficientes son: \( A = 4 \), \( B = -9 \), \( C = -16 \), \( D = -54 \), y \( E = -101 \).
Aplicamos la fórmula para hallar el centro:
$$ \left(p, q\right) = \left(-\frac{C}{2A}, - \frac{D}{2B}\right) $$
$$ \left(p, q\right) = \left(-\frac{-16}{2 \cdot 4}, - \frac{-54}{2 \cdot (-9)}\right) $$
$$ \left(p, q\right) = \left(\frac{16}{8}, - \frac{54}{18}\right) $$
$$ \left(p, q\right) = \left(2, -3\right) $$
Demostración
Partimos de la forma general de una hipérbola no centrada en el origen:
$$ Ax^2 + By^2 + Cx + Dy + E = 0 $$
Agrupamos los términos cuadráticos y lineales:
$$ (Ax^2 + Cx) + (By^2 + Dy) = -E $$
Luego completamos el cuadrado para los términos en \(x\) y en \(y\):
- Para los términos en \(x\):
Factorizamos \(A\) en el binomio \(Ax^2 + Cx\): $$
A\left(x^2 + \frac{C}{A}x\right) $$ Completamos el cuadrado añadiendo y restando \(\left(\frac{C}{2A}\right)^2\): $$
A\left(x^2 + \frac{C}{A}x + \left(\frac{C}{2A}\right)^2 - \left(\frac{C}{2A}\right)^2\right) = A\left(\left(x + \frac{C}{2A}\right)^2 - \left(\frac{C}{2A}\right)^2\right) $$ Que se reduce a: $$ A\left(x + \frac{C}{2A}\right)^2 - A\left(\frac{C}{2A}\right)^2 $$ - Para los términos en \(y\):
Factorizamos \(B\) en el binomio \(By^2 + Dy\): $$ B\left(y^2 + \frac{D}{B}y\right) $$ Completamos el cuadrado sumando y restando \(\left(\frac{D}{2B}\right)^2\): $$ B\left(y^2 + \frac{D}{B}y + \left(\frac{D}{2B}\right)^2 - \left(\frac{D}{2B}\right)^2\right) = B\left(\left(y + \frac{D}{2B}\right)^2 - \left(\frac{D}{2B}\right)^2\right) $$ Que se reduce a: $$ B\left(y + \frac{D}{2B}\right)^2 - B\left(\frac{D}{2B}\right)^2 $$
Sustituimos las expresiones desarrolladas en la ecuación original:
$$ Ax^2 + Cx + By^2 + Dy = -E $$
$$ (Ax^2 + Cx) + (By^2 + Dy) = -E $$
$$ A\left(x^2 + \frac{C}{A}x\right) + B\left(y^2 + \frac{D}{B}y\right) = -E $$
$$ A\left(x + \frac{C}{2A}\right)^2 - A\left(\frac{C}{2A}\right)^2 + B\left(y + \frac{D}{2B}\right)^2 - B\left(\frac{D}{2B}\right)^2 = -E $$
$$ A\left(x + \frac{C}{2A}\right)^2 + B\left(y + \frac{D}{2B}\right)^2 = E + A\left(\frac{C}{2A}\right)^2 + B\left(\frac{D}{2B}\right)^2 $$
Esta expresión muestra claramente el desplazamiento, y confirma que el centro de la hipérbola está en:
$$ \left(-\frac{C}{2A}, -\frac{D}{2B}\right) $$
Es decir:
$$ \left(p, q\right) = \left(-\frac{C}{2A}, - \frac{D}{2B}\right) $$
Ejes de simetría
Los ejes de simetría de una hipérbola que no está centrada en el origen, representada por la ecuación $$ Ax^2 + By^2 + Cx + Dy + E = 0 $$, están determinados por las coordenadas del centro \( (p,q) \), y sus ecuaciones son: $$ x = p = -\frac{C}{2A} $$ $$ y = q = - \frac{D}{2B} $$
Ejemplo
Retomemos la ecuación general de una hipérbola desplazada:
$$ 4x^2 - 9y^2 - 16x - 54y - 101 = 0 $$
En este caso: \( A = 4 \), \( B = -9 \), \( C = -16 \), \( D = -54 \), \( E = -101 \).
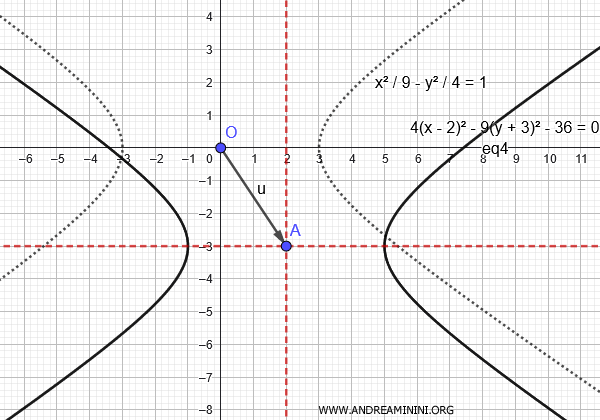
Las ecuaciones de los ejes de simetría son:
$$ x = p = -\frac{C}{2A} = -\frac{-16}{2 \cdot 4} = 2 $$
$$ y = q = -\frac{D}{2B} = -\frac{-54}{2 \cdot (-9)} = -3 $$
Demostración
Los ejes de simetría de una hipérbola son las rectas que pasan por su centro y coinciden con sus ejes principales. Si la cónica no está rotada, estos ejes son paralelos a los ejes coordenados.
En ese caso, las ecuaciones de los ejes de simetría son simplemente:
$$ x = p $$
$$ y = q $$
donde \((p, q)\) son las coordenadas del centro.
Nota: Si la hipérbola está rotada, las ecuaciones de los ejes de simetría se determinan mediante una transformación que involucra el ángulo de rotación \(\theta\), el cual puede deducirse a partir de los coeficientes \(A\), \(B\) y del término mixto (si lo hay) presente en la ecuación general. En estos casos, es necesario resolver un sistema para identificar la dirección de los ejes.
Y así sucesivamente.