Cálculo de la ecuación de una hipérbola a partir de una asíntota y un foco

Para determinar la ecuación de una hipérbola centrada en el origen, conocer la posición de uno de sus focos permite establecer si el eje transversal se encuentra sobre el eje x o sobre el eje y.

• Si el foco está en $ F(c;0) $, el eje transversal es el eje x y la ecuación de la hipérbola es $$ \frac{x^2}{a^2} - \frac{y^2}{b^2} = 1 $$
• Si el foco está en $ F(0;c) $, el eje transversal es el eje y, y la ecuación correspondiente es $$ \frac{x^2}{a^2} - \frac{y^2}{b^2} = -1 $$

En ambos casos, las ecuaciones de las asíntotas vienen dadas por:

$$ y = \pm \frac{b}{a} x $$

Además, la relación fundamental entre los semiejes $ a $ y $ b $ y la distancia $ c $ desde el centro al foco es:

$$ c^2 = a^2 + b^2 $$

Con estos elementos, es posible deducir la ecuación de la hipérbola.

Ejemplo práctico

Consideremos una hipérbola con uno de sus focos en

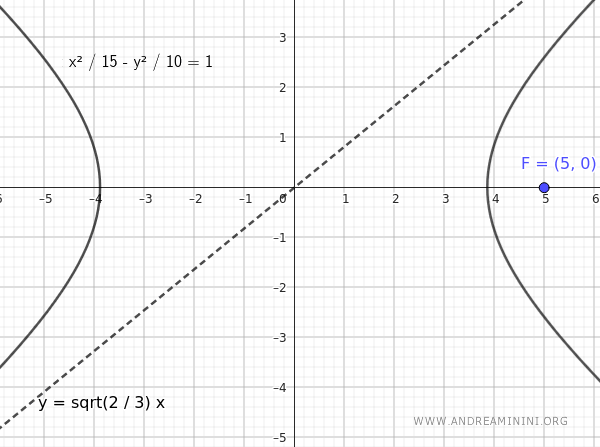
$$ F(c;0) = F(5;0) $$

y una asíntota dada por

$$ y = \sqrt{\frac{2}{3}} x $$

Como el foco se encuentra sobre el eje x, la ecuación de la hipérbola es:

$$ \frac{x^2}{a^2} - \frac{y^2}{b^2} = 1 $$

Para hallar los valores de los semiejes $ a $ y $ b $, planteamos un sistema que combina la pendiente de la asíntota con la relación entre los semiejes y la distancia focal:

$$ \begin{cases} y = \pm \frac{b}{a} x \\ \\ c^2 = a^2 + b^2 \end{cases} $$

Sabemos que la pendiente de la asíntota es $ \sqrt{\frac{2}{3}} $ y que $ c = 5 $, por tanto:

$$ \begin{cases} \sqrt{\frac{2}{3}} = \frac{b}{a} \\ \\ 25 = a^2 + b^2 \end{cases} $$

De la primera ecuación despejamos $ b $ en función de $ a $:

$$ \begin{cases} b = \sqrt{\frac{2}{3}} \cdot a \\ \\ 25 = a^2 + b^2 \end{cases} $$

Sustituyendo en la segunda ecuación:

$$ 25 = a^2 + \left(\sqrt{\frac{2}{3}} \cdot a\right)^2 $$

$$ 25 = a^2 + \frac{2}{3} a^2 $$

$$ 25 = \frac{5a^2}{3} $$

$$ a^2 = 25 \cdot \frac{3}{5} = 15 $$

$$ a = \sqrt{15} $$

Ahora sustituimos el valor de $ a $ en la expresión de $ b $:

$$ b = \sqrt{\frac{2}{3}} \cdot \sqrt{15} = \sqrt{ \frac{2 \cdot 15}{3} } = \sqrt{10} $$

Por tanto, los valores de los semiejes son $ a = \sqrt{15} $ y $ b = \sqrt{10} $. Sustituyéndolos en la ecuación canónica obtenemos:

$$ \frac{x^2}{(\sqrt{15})^2} - \frac{y^2}{(\sqrt{10})^2} = 1 $$

$$ \frac{x^2}{15} - \frac{y^2}{10} = 1 $$

Esta es la ecuación de la hipérbola con foco en $ F(5;0) $ y una asíntota con pendiente $ \sqrt{\frac{2}{3}} $.

Así es como se obtiene la ecuación buscada.