Eliminación del término mixto xy en las cónicas

Para suprimir el término mixto $xy$ en una cónica, basta con girar los ejes un ángulo $\alpha$ tal que $$\tan 2\alpha = \frac{B}{A - C}$$ donde $A, B, C$ son los coeficientes de la ecuación general. Los ángulos de rotación que cumplen esta condición son $$ \alpha = \tfrac{1}{2} \arctan \left(\frac{B}{A - C}\right) + \tfrac{k\pi}{2} $$

Siempre existe algún ángulo de rotación que permite eliminar el término mixto $xy$ de la ecuación de una cónica.

El procedimiento para determinar este ángulo es el siguiente:

1. Identificar los coeficientes $(A, B, C)$ en la ecuación general de la cónica: $$ Ax^2 + Bxy + Cy^2 + Dx + Ey + F = 0 $$
2. Aplicar la fórmula del ángulo de rotación: $$ \tan 2\alpha = \frac{B}{A - C} $$

   Nota. Si el denominador $A - C$ es cero, la tangente no está definida (el ángulo es vertical). En este caso particular, la condición se reduce a $$ \cos 2\alpha = 0 \quad \Longrightarrow \quad 2\alpha = \tfrac{\pi}{2} + k\pi $$

3. Calcular el ángulo de rotación $ \alpha $ y escoger una de las soluciones: $$ \alpha = \tfrac{1}{2} \arctan \left(\frac{B}{A - C}\right) + \tfrac{k\pi}{2} $$
4. Rotar los ejes en el ángulo $ \alpha $ elegido: $$ \begin{cases} x = x'\cos\alpha - y'\sin\alpha \\ \\ y = x'\sin\alpha + y'\cos\alpha  \end{cases}$$
5. Reescribir la ecuación de la cónica. El término mixto $ x'y' $ desaparece.

Ejemplo resuelto

Veamos ahora un ejemplo concreto. Consideremos la siguiente ecuación cónica, que contiene un término mixto:

$$ 4x^2 + 8xy + 4y^2 + \sqrt{2} x - \sqrt{2} y = 0 $$

Los coeficientes son: $$ A=4, \ B=8, \ C=4, \ D=\sqrt{2}, \ E=-\sqrt{2}, \ F=0$$

Calculemos el ángulo que elimina $xy$ aplicando la fórmula:

$$ \tan 2\alpha = \frac{B}{A-C} $$

Como $A-C=0 $, $\tan 2\alpha$ no está definida.

En este caso, recurrimos a la condición alternativa $ \cos 2\alpha=0$, que conduce a:

$$ 2\alpha = \arccos 0 $$

$$ 2 \alpha = \frac{\pi}{2}+k\pi $$

$$  \alpha=\frac{\pi}{4}+k\frac{\pi}{2} $$

Para simplificar, tomamos $\alpha=\frac{\pi}{4}$ y efectuamos la rotación:

$$ \begin{cases} x = x'\cos\alpha + y'\sin\alpha \\ \\ y = -x'\sin\alpha + y'\cos\alpha \end{cases} $$

$$ \begin{cases} x = x'\cos \frac{\pi}{4} + y'\sin \frac{\pi}{4} \\ \\ y = -x'\sin \frac{\pi}{4} + y'\cos \frac{\pi}{4} \end{cases} $$

Dado que $ \cos \frac{\pi}{4} = \frac{\sqrt{2}}{2} $ y $ \sin \frac{\pi}{4} = \frac{\sqrt{2}}{2} $:

$$ \begin{cases} x = x' \frac{\sqrt{2}}{2} + y' \frac{\sqrt{2}}{2} \\ \\ y = -x' \frac{\sqrt{2}}{2} + y' \frac{\sqrt{2}}{2} \end{cases} $$

$$ \begin{cases} x = \frac{\sqrt{2}}{2} (x' + y') \\ \\ y =  \frac{\sqrt{2}}{2} ( y' -x' ) \end{cases} $$

Sustituyendo $ x $ y $ y $ en la ecuación original obtenemos:

$$ 4x^2 + 8xy + 4y^2 + \sqrt{2} x - \sqrt{2} y = 0 $$

Ahora expandimos los términos cuadráticos $ 4x^2, 8xy , 4y^2 $ y los lineales $ \sqrt{2} x, \sqrt{2} y $:

• $ 4x^2 = 4 ( \frac{\sqrt{2}}{2} (x' + y') )^2 =  2x'^2+4x'y'+2y'^2 $
• $ 8xy = 8 ( \frac{\sqrt{2}}{2} (x' + y') ) (  \frac{\sqrt{2}}{2} ( y' -x' ) ) = 4y'^2 -4x'^2 $
• $ 4y^2 =  4 ( \frac{\sqrt{2}}{2} (y' -x') )^2 = 2x'^2-4x'y'+2y'^2 $
• $ \sqrt{2} x = \sqrt{2}  \frac{\sqrt{2}}{2} (x' + y') = x'+y' $
• $ - \sqrt{2} y = - \sqrt{2}  \frac{\sqrt{2}}{2} (y' -x' ) = x'-y' $

Reuniendo todos los términos, la ecuación queda:

$$ (2x'^2+4x'y'+2y'^2) + ( 4y'^2 -4x'^2 )  + ( 2x'^2 -4x'y'+2y'^2 ) + (x'+y' ) + (x'-y' ) = 0  $$

$$ 2x'^2+4x'y'+2y'^2 + 4y'^2 -4x'^2  + 2x'^2 -4x'y'+2y'^2 + x'+y' + x'-y'  = 0  $$

$$ x^2 (2-4+2) + y'^2 (2 +4 +2) + x'y' (4-4) + 2x'  = 0  $$

$$ 0 \cdot x^2 + 8 \cdot  y'^2 + 0 \cdot x'y' + 2x' = 0  $$

$$ 8 y'^2 + 2x' = 0  $$

En el sistema rotado con $\alpha=\frac{\pi}{4}$, el término mixto $ xy $ desaparece.

$$ 2x' = - 8 y'^2   $$

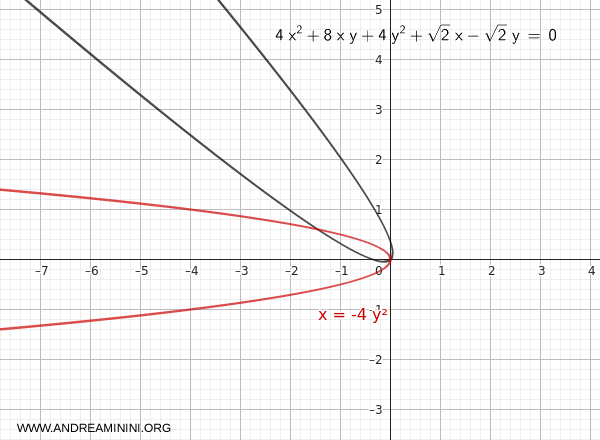
$$ x'=-4 y'^2 $$

Después de la rotación, la parábola tiene su vértice en el origen, su eje es paralelo al eje $x'$ y se abre hacia la izquierda:

Demostración

Comenzamos con la ecuación general de una cónica:

$$ Ax^2 + Bxy + Cy^2 + Dx + Ey + F = 0 $$

El objetivo es determinar el ángulo de rotación $ \alpha $ que elimine el coeficiente $ B $, responsable del término mixto $ xy $.

En geometría analítica, una rotación de ejes se expresa así:

$$ \begin{cases} x = x'\cos\alpha - y'\sin\alpha \\ y = x'\sin\alpha + y'\cos\alpha \end{cases} $$

Sustituyendo $ x $ y $ y $ en la ecuación de la cónica, desarrollamos cada término:

• El término $ Ax^2 $: $$ \begin{aligned} Ax^2 &= A\,(x' \cos \alpha - y' \sin \alpha)^2 \\ &= A\,(x'^2 \cos^2 \alpha - 2x'y' \sin \alpha \cos \alpha + y'^2 \sin^2 \alpha) \end{aligned} $$
• El término $ Bxy $: $$ \begin{aligned} Bxy &= B\,(x' \cos \alpha - y' \sin \alpha)(x' \sin \alpha + y' \cos \alpha) \\ &= B\,(x'^2 \cos \alpha \sin \alpha + x'y'(\cos^2 \alpha - \sin^2 \alpha) - y'^2 \sin \alpha \cos \alpha) \end{aligned} $$
• El término $ Cy^2 $: $$ \begin{aligned} Cy^2 &= C\,(x' \sin \alpha + y' \cos \alpha)^2 \\ &= C\,(x'^2 \sin^2 \alpha + 2x'y' \sin \alpha \cos \alpha + y'^2 \cos^2 \alpha) \end{aligned} $$
• El término $ Dx $: $$ \begin{aligned} Dx &= D\,(x'\cos\alpha - y'\sin\alpha) \\ &= (D\cos\alpha)\,x' + (-D\sin\alpha)\,y' \end{aligned} $$
• El término $ Ey $: $$ \begin{aligned} Ey &= E\,(x'\sin\alpha + y'\cos\alpha) \\ &= (E\sin\alpha)\,x' + (E\cos\alpha)\,y' \end{aligned} $$

Reunimos ahora los coeficientes del término mixto $ x'y' $:

$$ B' = -2A x'y' \sin \alpha \cos \alpha + B x'y' ( \cos^2 \alpha - \sin^2 \alpha) + 2C x'y' \sin \alpha \cos \alpha $$

$$ B' = x'y' \cdot \big( -2A \sin \alpha \cos \alpha + B ( \cos^2 \alpha - \sin^2 \alpha) + 2C \sin \alpha \cos \alpha \big) $$

Por la propiedad del producto nulo, $ B' = 0 $ si y solo si uno de los factores se anula.

El primer factor, $ x'y'=0 $, es trivial. La condición relevante proviene del segundo factor:

$$ - 2A \sin \alpha \cos \alpha + B ( \cos^2 \alpha - \sin^2 \alpha) + 2C \sin \alpha \cos \alpha = 0 $$

Reordenando términos obtenemos:

$$ (2C - 2A) \sin \alpha \cos \alpha + B ( \cos^2 \alpha - \sin^2 \alpha) = 0 $$

$$ (C - A) \cdot 2 \sin \alpha \cos \alpha + B ( \cos^2 \alpha - \sin^2 \alpha) = 0 $$

Aplicando las identidades de ángulo doble, $ 2 \sin \alpha \cos \alpha = \sin 2 \alpha $ y $ \cos^2 \alpha - \sin^2 \alpha = \cos 2 \alpha $, se obtiene:

$$ (C - A) \sin 2 \alpha + B \cos 2 \alpha = 0 $$

$$ (C - A) \sin 2 \alpha = - B \cos 2 \alpha $$

Dividiendo entre $ \cos 2 \alpha $ resulta:

$$ (C - A) \frac{ \sin 2 \alpha }{ \cos 2 \alpha } = - B $$

Como $ \tfrac{\sin \theta}{\cos \theta} = \tan \theta $, concluimos que:

$$ (C - A) \tan 2 \alpha = - B $$

$$ \tan 2 \alpha = \frac{- B }{C-A } $$

Multiplicando numerador y denominador por $ -1 $ llegamos a:

$$ \tan 2 \alpha = \frac{ B }{A-C } $$

Así, siempre que $ \tan 2 \alpha = \tfrac{ B }{A-C } $, el coeficiente $ B' $ del término mixto se anula. Esta es la condición necesaria para eliminarlo.

A partir de esta relación se sigue que:

$$ 2\alpha = \arctan \left(\frac{B}{A - C}\right) + k\pi, \qquad k \in \mathbb{Z} $$

De donde se deduce:

$$ \alpha = \tfrac{1}{2} \arctan \left(\frac{B}{A - C}\right) + \tfrac{k\pi}{2} $$

En otras palabras, no existe una única solución para $\alpha$, sino una familia de ángulos que difieren en $\tfrac{\pi}{2}$.

En la práctica, se suele elegir la solución comprendida entre $-\tfrac{\pi}{4}$ y $\tfrac{\pi}{4}$.

Con ello queda establecida la demostración.