Ecuación de la Parábola

La forma general de la ecuación de una parábola cuyo eje de simetría es paralelo al eje y es: $$ y = ax^2 + bx + c $$ donde \( a \), \( b \) y \( c \) son coeficientes reales constantes, con \( a \neq 0 \).

El coeficiente \( a \) desempeña un papel clave en el análisis de la parábola.

El valor absoluto \( |a| \) determina la apertura de la parábola: cuanto mayor sea \( |a| \), más estrecha será la curva respecto a su eje.

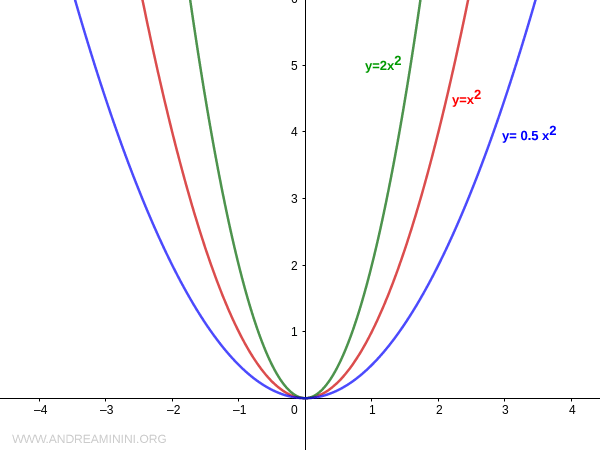
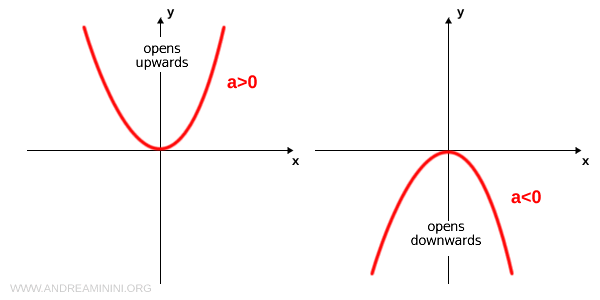
Además, el signo de \( a \) define la dirección de la concavidad de la parábola:

• Si \( a > 0 \), la parábola abre hacia arriba (concavidad positiva).
• Si \( a < 0 \), la parábola abre hacia abajo (concavidad negativa).

Cuando el eje de simetría es horizontal, la ecuación estándar se expresa como: $$ x = ay^2 + by + c $$

Los elementos característicos de una parábola son los siguientes:

• Foco
  El foco \( F \) es un punto fijo situado en el interior de la parábola. Sus coordenadas están dadas por:
  \[ F \begin{pmatrix} -\frac{b}{2a}, \frac{1-\Delta}{4a} \end{pmatrix} \] donde \( a \), \( b \) y \( c \) son los coeficientes de la ecuación \( y = ax^2 + bx + c \), y el discriminante es \( \Delta = b^2 - 4ac \).
• Directriz
  La directriz \( d \) es una recta fija exterior a la parábola. Su ecuación es: $$ y = - \frac{1+\Delta}{4a} $$
• Eje
  El eje de la parábola es la recta perpendicular a la directriz \( d \) que pasa por el foco \( F \). Coincide con el eje de simetría, dividiendo la parábola en dos mitades simétricas. Su ecuación es: $$ x = - \frac{b}{2a} $$
• Vértice
  El vértice \( V \) es el punto donde la parábola intersecta su eje de simetría. En él se alcanza el valor máximo o mínimo de la función, según el signo del coeficiente \( a \) en la ecuación \( y = ax^2 + bx + c \). Sus coordenadas son:
  \[ V \left( -\frac{b}{2a} , -\frac{\Delta}{4a} \right) \] donde \(\Delta = b^2 - 4ac\) representa el discriminante.

Casos Especiales de la Ecuación de la Parábola

La ecuación \( y = ax^2 + bx + c \) presenta formas particulares cuando los coeficientes \( b \) y/o \( c \) son iguales a cero.

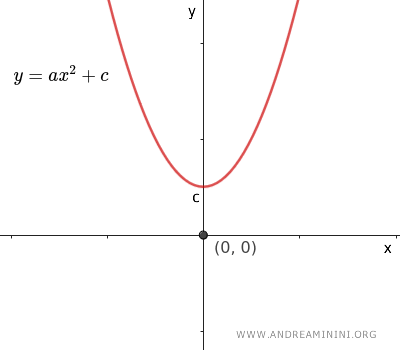
• Si \( b = 0 \), la ecuación se reduce a \( y = ax^2 + c \) y el eje de simetría coincide con el eje y.
  
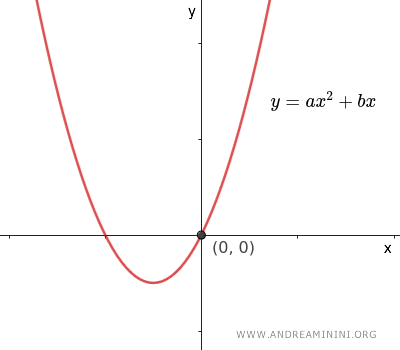
• Si \( c = 0 \), la ecuación se convierte en \( y = ax^2 + bx \), y la parábola pasa por el origen \( O(0,0) \) del plano cartesiano, ya que al sustituir \( x = 0 \), también se obtiene \( y = 0 \).
  
• Si \( b = 0 \) y \( c = 0 \), la ecuación se simplifica a \( y = ax^2 \), por lo que la parábola tiene su eje coincidiendo con el eje y y su vértice en el origen \( O(0,0) \).
  

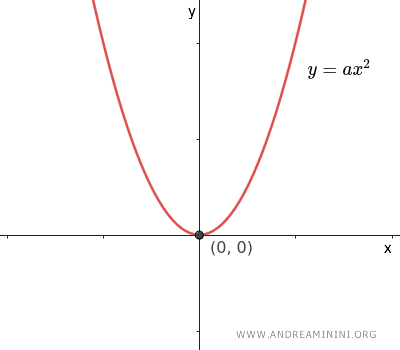
Ecuación de una Parábola con Eje sobre el Eje Y y Vértice en el Origen

La ecuación de una parábola cuyo eje de simetría coincide con el eje y y cuyo vértice se encuentra en el origen del plano cartesiano es: $$ y = ax^2 $$ donde \( a \ne 0 \) es un coeficiente real distinto de cero.

En este caso, el eje de simetría de la parábola es simplemente:

$$ x = 0 $$

Las coordenadas del foco \( F \) son:

$$ F \left(0; \frac{1}{4a} \right) $$

Y la ecuación de la directriz viene dada por:

$$ y = - \frac{1}{4a} $$

Nota: Una parábola con eje sobre el eje y y vértice en el origen toma únicamente valores no negativos cuando \( a > 0 \); en ese caso, el foco se encuentra por encima del vértice y la parábola se abre hacia arriba. Por el contrario, si \( a < 0 \), sus valores son no positivos, el foco se sitúa por debajo del vértice y la parábola se abre hacia abajo.

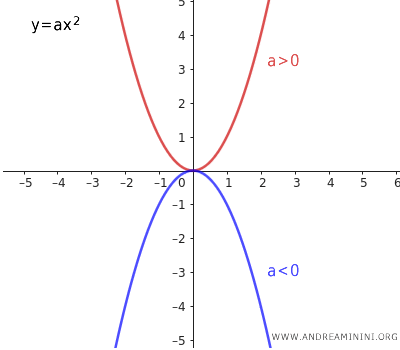
Se dice que dos parábolas son simétricas cuando tienen coeficientes \( a \) opuestos. Por ejemplo, las parábolas \( y = \frac{1}{8}x^2 \) y \( y = -\frac{1}{8}x^2 \) son simétricas respecto al eje x. Además de simétricas, estas parábolas son congruentes. En el caso particular en que \( a = 0 \), la parábola se reduce a la recta \( y = 0 \), que coincide con el eje x. A esta situación se le denomina parábola degenerada.

Ejemplo

Analicemos el siguiente ejemplo:

$$ y = \frac{1}{8} x^2 $$

Como \( a = \frac{1}{8} \), podemos calcular las coordenadas del foco:

$$ F \left(0; \frac{1}{4a} \right) $$

$$ F \left(0; \frac{1}{4 \cdot \frac{1}{8}} \right) $$

$$ F \left(0; \frac{1}{\frac{1}{2}} \right) $$

$$ F (0; 2) $$

La ecuación de la directriz es:

$$ y = - \frac{1}{4a} $$

$$ y = - \frac{1}{4 \cdot \frac{1}{8}} $$

$$ y = - \frac{1}{\frac{1}{2}} $$

$$ y = -2 $$

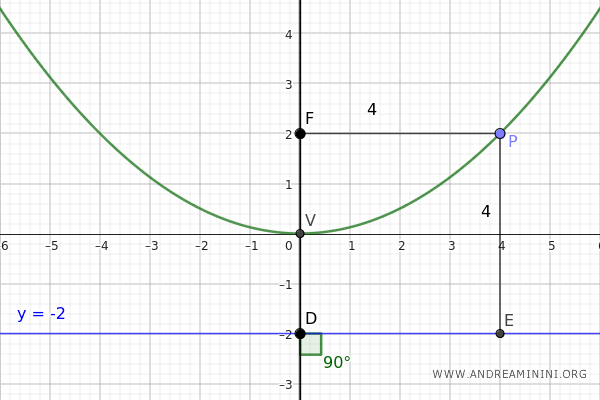
A continuación, se muestra la gráfica correspondiente a esta parábola:

Demostración

Partimos del supuesto de que el eje de la parábola coincide con el eje y y que su vértice \( V \) se encuentra en el origen del plano cartesiano.

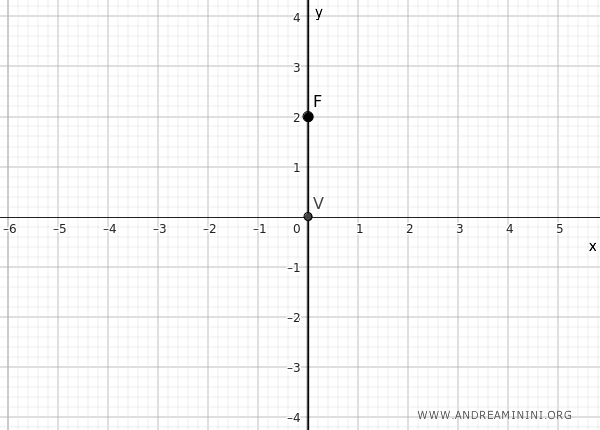
El foco \( F \) es un punto que se encuentra sobre el eje de simetría de la parábola, es decir, sobre el eje y.

Por definición, en una parábola, la distancia entre cualquier punto de la curva y el foco es igual a la distancia entre ese mismo punto y la directriz.

En este caso, el punto \( V \) es el único punto conocido de la parábola. Sin embargo, podemos deducir que la distancia VF es igual a OD, donde \( D \) es un punto situado sobre la directriz.

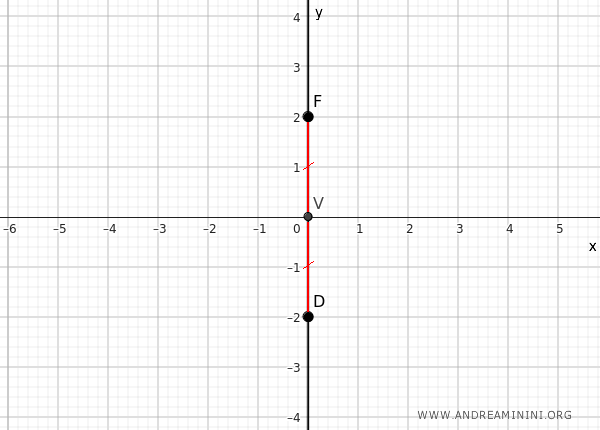
Dado que la directriz siempre es perpendicular al eje de la parábola, en este caso será paralela al eje x y pasará por el punto \( D \).

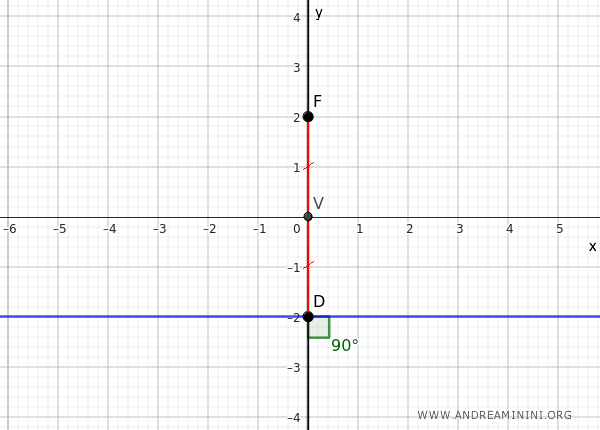
Así, la ecuación de la directriz es:

$$ y = -f $$

Donde \( f = VD \), y por construcción también \( f = VF \), ya que \( VD = VF \).

Consideremos ahora un punto cualquiera \( P \) sobre la parábola.

Según la definición, la distancia entre \( P \) y el foco debe ser igual a la distancia entre \( P \) y la directriz, es decir, \( PF = PE \).

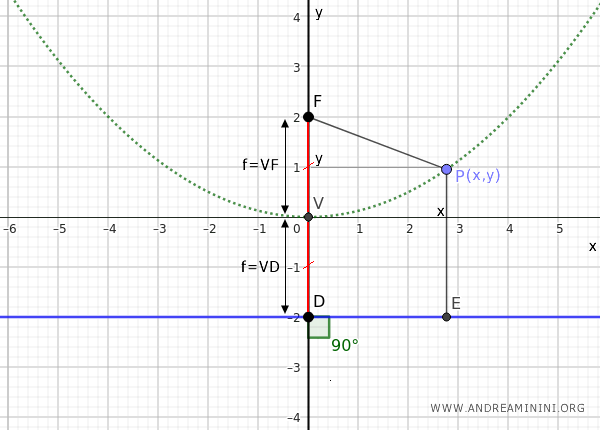
Entonces, se cumple:

$$ \overline{PF} = \overline{PE} $$

Podemos expresar \( \overline{PF} \) mediante la fórmula de la distancia euclídea entre dos puntos: $$ \overline{PF} = \sqrt{ x^2 + (f - y)^2 } $$ siendo \( f = VF \).

Entonces:

$$ \sqrt{ x^2 + (f - y)^2 } = \overline{PE} $$

La distancia \( \overline{PE} \) se puede expresar como: $$ \overline{PE} = | y + f | $$ ya que \( f = VD \).

De modo que obtenemos la igualdad:

$$ \sqrt{ x^2 + (f - y)^2 } = | y + f | $$

Elevamos ambos miembros al cuadrado para eliminar la raíz y el valor absoluto:

$$ \left( \sqrt{ x^2 + (f - y)^2 } \right)^2 = ( | y + f | )^2 $$

$$ x^2 + (f - y)^2 = (y + f)^2 $$

Desarrollamos ambos lados de la ecuación:

$$ x^2 + f^2 - 2fy + y^2 = y^2 + 2fy + f^2 $$

Simplificamos eliminando los términos comunes:

$$ x^2 - 4fy = 0 $$

Despejando \( y \), se obtiene la ecuación de la parábola:

$$ y = \frac{1}{4f} x^2 $$

Si definimos \( a = \frac{1}{4f} \), la ecuación puede escribirse como:

$$ y = ax^2 $$

Como \( f \ne 0 \), para evitar una división por cero, se deduce que también \( a \ne 0 \). Por tanto, el coeficiente \( a \) debe ser siempre distinto de cero.

A partir de la relación \( a = \frac{1}{4f} \), podemos expresar \( f \) (la ordenada del foco) como:

$$ f = \frac{1}{4a} $$

Y como el eje de la parábola es el eje y, la abscisa del foco es cero.

Así, las coordenadas del foco en el plano cartesiano son:

$$ F(x, y) = \left( 0, \frac{1}{4a} \right) $$

Finalmente, como la directriz está dada por:

$$ y = -f $$

Y reemplazando \( f = \frac{1}{4a} \), se obtiene la ecuación explícita de la directriz:

$$ y = -\frac{1}{4a} $$

Con esto, hemos deducido de forma rigurosa todas las expresiones fundamentales que definen una parábola cuyo eje coincide con el eje y y cuyo vértice está en el origen del plano.

Ecuación de una Parábola con Eje Paralelo al Eje Y

La ecuación de una parábola cuyo eje es paralelo al eje y y cuyo vértice se encuentra en un punto cualquiera del plano cartesiano es: $$ y = ax^2 + bx + c $$ donde \( a \ne 0 \). Alternativamente, puede expresarse en forma canónica con vértice \( (h, k) \): $$ y = a(x - h)^2 + k $$ o en forma estándar, donde \( p \) representa la distancia del vértice al foco: $$ (x - h)^2 = 4p(y - k) $$

Toda parábola de la forma \( y = ax^2 + bx + c \), con eje paralelo al eje y y vértice en \( V(x_v, y_v) \), se obtiene mediante la traslación de la parábola básica \( y = ax^2 \), cuyo vértice está en el origen y eje sobre el eje y.

$$ y - y_v = a(x - x_v)^2 $$

El eje de simetría es:

$$ x = -\frac{b}{2a} $$

Las coordenadas del vértice son:

$$ V \begin{pmatrix} -\frac{b}{2a},\ -\frac{\Delta}{4a} \end{pmatrix} $$

donde \( \Delta = b^2 - 4ac \) es el discriminante.

Las coordenadas del foco \( F \) son:

$$ F \begin{pmatrix} -\frac{b}{2a},\ \frac{1 - \Delta}{4a} \end{pmatrix} $$

La ecuación de la directriz es:

$$ y = -\frac{1 + \Delta}{4a} $$

Nota: Toda ecuación del tipo \( y = ax^2 + bx + c \), con \( a \ne 0 \), describe una parábola cuyo eje es paralelo al eje y, y viceversa. Estas parábolas no son más que traslaciones de la parábola \( y = ax^2 \), cuyo eje coincide exactamente con el eje y.

Ejemplo

Consideremos la parábola:

$$ y = 2x^2 - 4x - 1 $$

Con \( a = 2 \), \( b = -4 \), \( c = -1 \) y \( \Delta = b^2 - 4ac = 24 \), obtenemos el vértice:

$$ V \begin{pmatrix} -\frac{-4}{2 \cdot 2},\ -\frac{24}{4 \cdot 2} \end{pmatrix} = V \begin{pmatrix} 1,\ -3 \end{pmatrix} $$

La ecuación de la directriz será:

$$ y = -\frac{1 + 24}{4 \cdot 2} = -\frac{25}{8} $$

Y las coordenadas del foco son:

$$ F \begin{pmatrix} -\frac{-4}{2 \cdot 2},\ \frac{1 - 24}{4 \cdot 2} \end{pmatrix} = F \begin{pmatrix} 1,\ -\frac{23}{8} \end{pmatrix} $$

En el siguiente gráfico puede observarse que cada punto de la parábola es equidistante del foco \( F \) y de la directriz:

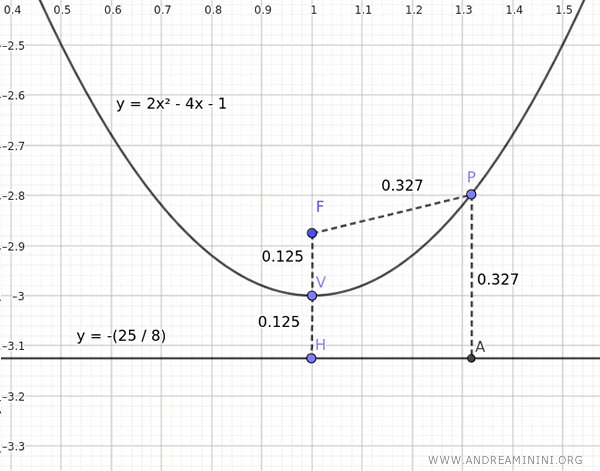
Nota: La distancia entre el origen \( O(0,0) \) y el vértice \( V(1, -3) \) está representada por el vector $$ \vec{v} = \begin{pmatrix} 1,\ -3 \end{pmatrix} $$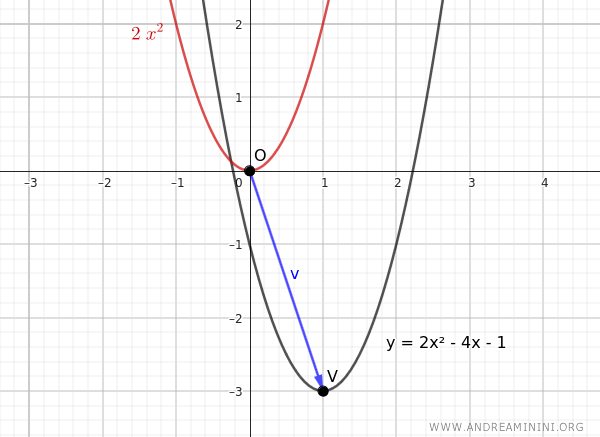
Esto demuestra que la parábola \( y = 2x^2 - 4x - 1 \) es una traslación de la parábola \( y = 2x^2 \), con el mismo coeficiente \( a = 2 \).

Aplicando la fórmula de traslación:

$$ y - y_v = a(x - x_v)^2 $$

Con \( x_v = 1 \) y \( y_v = -3 \):

$$ y + 3 = 2(x - 1)^2 $$

Desarrollando la expresión:

$$ y = 2(x^2 - 2x + 1) - 3 = 2x^2 - 4x + 2 - 3 = 2x^2 - 4x - 1 $$

Queda así confirmado que \( y = 2x^2 - 4x - 1 \) es la traslación de la parábola \( y = 2x^2 \). Estas dos parábolas son congruentes, ya que pueden superponerse punto a punto mediante una transformación rígida, es decir, una isometría que no altera su forma.

Demostración

Para demostrar la ecuación \( y = ax^2 + bx + c \), partimos de la siguiente premisa:

Toda parábola con eje paralelo al eje y puede obtenerse mediante la traslación de una parábola del tipo \( y = ax^2 \), cuyo eje coincide con el eje y.

$$ y = ax^2 $$

En general, la traslación de un punto \( (x, y) \rightarrow (x', y') \) en el plano se describe mediante la siguiente transformación isométrica:

$$ \begin{cases} x' = x + x_v \\ \\ y' = y + y_v \end{cases} $$

donde \( (x, y) \) son las coordenadas del punto original y \( (x', y') \) las del punto trasladado.

Los valores \( x_v \) y \( y_v \) representan las componentes del vector de traslación \( \vec{v} = \begin{pmatrix} x_v \\ y_v \end{pmatrix} \).

Invirtiendo el sistema, obtenemos las expresiones de \( x \) e \( y \):

$$ \begin{cases} x = x' - x_v \\ \\ y = y' - y_v \end{cases} $$

Sustituimos en la ecuación de la parábola con vértice en el origen:

$$ y = ax^2 $$

$$ y' - y_v = a(x' - x_v)^2 $$

Suprimiendo los apóstrofos por simplicidad, obtenemos la ecuación de una parábola con eje paralelo al eje y y vértice en \( V(x_v, y_v) \):

$$ y - y_v = a(x - x_v)^2 $$

Resolviendo para \( y \):

$$ y = a(x^2 - 2x x_v + x_v^2) + y_v $$

$$ y = ax^2 - 2a x x_v + a x_v^2 + y_v $$

Definimos los coeficientes \( b = -2a x_v \) y \( c = a x_v^2 + y_v \), con lo cual la ecuación se transforma en:

$$ y = ax^2 + bx + c $$

Hemos demostrado así que toda parábola con eje paralelo al eje y puede representarse mediante una ecuación cuadrática de la forma \( y = ax^2 + bx + c \).

A partir de \( b = -2a x_v \), obtenemos la abscisa del vértice:

$$ x_v = -\frac{b}{2a} $$

Y de \( c = a x_v^2 + y_v \), deducimos la ordenada:

$$ y_v = c - a x_v^2 $$

$$ y_v = c - a \left( -\frac{b}{2a} \right)^2 $$

$$ y_v = c - \frac{b^2}{4a} $$

Ya que \( \Delta = b^2 - 4ac \), se sigue que \( -\Delta = 4ac - b^2 \), por lo tanto:

$$ y_v = \frac{-\Delta}{4a} $$

Nota: Para probar que toda ecuación \( y = ax^2 + bx + c \) representa una parábola, basta trasladar la parábola \( y = ax^2 \) mediante un vector \( \vec{v} = (x_v, y_v) \):

Sabiendo que \( x_v = -\frac{b}{2a} \) y \( y_v = -\frac{\Delta}{4a} \):

$$ y - \frac{\Delta}{4a} = a\left(x - \frac{b}{2a} \right)^2 $$

Desarrollando el cuadrado:

$$ y = a\left[x^2 - 2x \cdot \frac{b}{2a} + \left( \frac{b}{2a} \right)^2 \right] + \frac{\Delta}{4a} $$

$$ y = ax^2 - bx + \frac{b^2}{4a} + \frac{\Delta}{4a} $$

Dado que \( \Delta = b^2 - 4ac \):

$$ y = ax^2 - bx + \frac{b^2}{4a} + \frac{b^2 - 4ac}{4a} $$

$$ y = ax^2 - bx + \frac{2b^2}{4a} - c $$

$$ y = ax^2 - bx + \frac{b^2}{2a} - c $$

Esta última expresión es también una parábola. Si definimos \( b' = -b \) y \( c' = \frac{b^2}{2a} - c \), la ecuación toma la forma canónica:

$$ y = ax^2 + b'x + c' $$

En conclusión, cualquier parábola con eje paralelo al eje y puede obtenerse como una traslación de la parábola \( y = ax^2 \) y su ecuación general es \( y = ax^2 + bx + c \).

Ecuación de una Parábola con Eje Paralelo al Eje X

La ecuación de una parábola cuyo eje es paralelo al eje x y cuyo vértice se encuentra en un punto cualquiera del plano cartesiano es: $$ x = ay^2 + by + c $$ donde \( a \ne 0 \). También puede expresarse en forma canónica, con vértice en \((h, k)\): $$ x = a(y - k)^2 + h $$ o en forma estándar, donde \( p \) representa la distancia entre el foco y el vértice: $$ (y - k)^2 = 4p(x - h) $$

El eje de simetría de la parábola está dado por:

$$ y = -\frac{b}{2a} $$

La ecuación de la directriz es:

$$ x = -\frac{1 + \Delta}{4a} $$

donde el discriminante es \( \Delta = b^2 - 4ac \).

Las coordenadas del foco son:

$$ F \left( \frac{1 - \Delta}{4a},\ -\frac{b}{2a} \right) $$

Y las del vértice:

$$ V \left( -\frac{\Delta}{4a},\ -\frac{b}{2a} \right) $$

Resumen de las fórmulas principales:

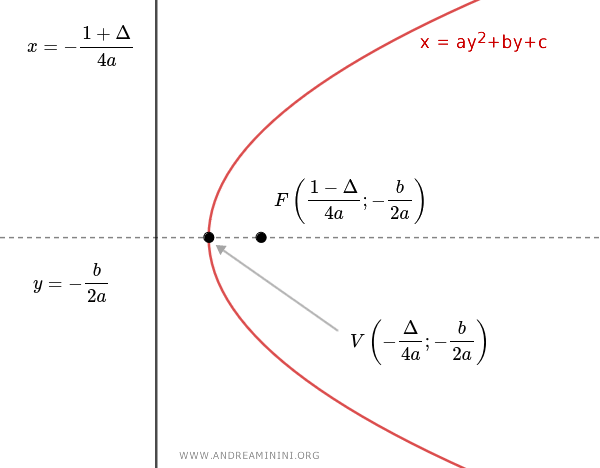
Nota: En este tipo de parábolas, el signo del coeficiente \( a \) determina la orientación de la concavidad. Si \( a > 0 \), la parábola se abre hacia la derecha (eje x positivo); si \( a < 0 \), se abre hacia la izquierda (eje x negativo). Además, el valor absoluto de \( a \) influye en la amplitud de la parábola con respecto a su eje de simetría: cuanto mayor sea \( |a| \), más estrecha será la parábola.

Ejemplo

Consideremos la parábola:

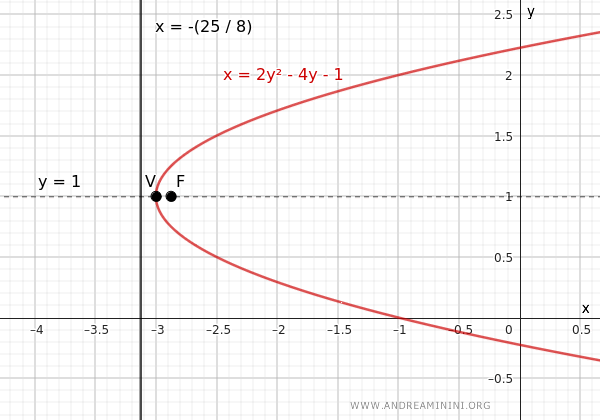
$$ x = 2y^2 - 4y - 1 $$

Sus coeficientes son \( a = 2 \), \( b = -4 \), \( c = -1 \), y el discriminante resulta ser:

$$ \Delta = b^2 - 4ac = (-4)^2 - 4 \cdot 2 \cdot (-1) = 16 + 8 = 24 $$

El eje de simetría es:

$$ y = -\frac{b}{2a} = -\frac{-4}{4} = 1 $$

La ecuación de la directriz es:

$$ x = -\frac{1 + \Delta}{4a} = -\frac{25}{8} $$

El foco se encuentra en las coordenadas:

$$ F \left( \frac{1 - \Delta}{4a},\ -\frac{b}{2a} \right) = F \left( \frac{-23}{8},\ 1 \right) $$

Y el vértice está en:

$$ V \left( -\frac{\Delta}{4a},\ -\frac{b}{2a} \right) = V \left( -3,\ 1 \right) $$

A continuación, se muestra el gráfico de la parábola, donde puede comprobarse que cada punto es equidistante del foco y de la directriz:

Demostración

Consideremos una parábola cuyo eje de simetría es paralelo al eje y:

$$ y = ax^2 + bx + c $$

Para transformarla en una parábola con eje paralelo al eje x, aplicamos una simetría axial respecto a la bisectriz de los cuadrantes primero y tercero del plano cartesiano:

$$ \begin{cases} x' = y \\ \\ y' = x \end{cases} $$

Donde \( (x', y') \) representan las coordenadas transformadas, y \( (x, y) \) las coordenadas originales.

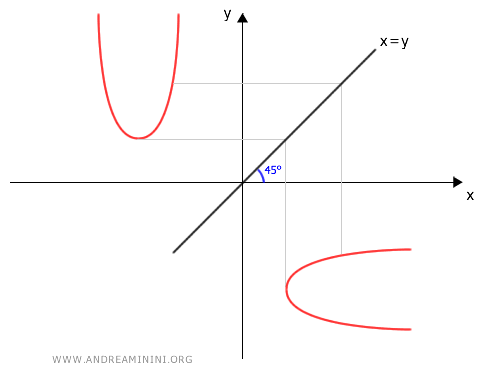
Aplicamos esta simetría a la ecuación de la parábola:

$$ y = ax^2 + bx + c $$

Sustituyendo \( x' = y \) y \( y' = x \), obtenemos:

$$ x' = a(y')^2 + b y' + c $$

Eliminando los apóstrofos por conveniencia, la ecuación resultante es:

$$ x = a y^2 + b y + c $$

Esta es la ecuación de una parábola cuyo eje de simetría es paralelo al eje x.

Las fórmulas para calcular las coordenadas del vértice, el foco, la directriz, etc., se derivan de manera análoga, aplicando esta misma simetría axial.

Nota: La ecuación \( x = ay^2 + by + c \) no define una función, ya que a un mismo valor de \( x \) pueden corresponder dos valores distintos de \( y \), excepto en el vértice. Por lo tanto, no puede considerarse una función en sentido estricto.

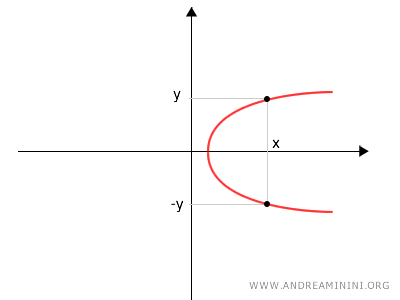
Cómo determinar la ecuación de una parábola

Para hallar la ecuación de una parábola, es necesario disponer de ciertos datos clave, que pueden variar según la forma elegida para la ecuación.

Las formas más comunes son:

• Parábola vertical
  Con eje de simetría paralelo al eje y: $$ y = ax^2 + bx + c $$
• Parábola horizontal
  Con eje de simetría paralelo al eje x: $$ x = ay^2 + by + c $$

Para determinar los coeficientes \( a \), \( b \) y \( c \), se necesitan al menos tres condiciones independientes, que pueden incluir puntos por los que pasa la parábola o elementos geométricos característicos como el vértice, el foco o la directriz.

Algunos de los casos más habituales son:

• Tres puntos distintos
  Conociendo las coordenadas de tres puntos distintos de la parábola, se puede resolver un sistema de ecuaciones para obtener los coeficientes.
• Vértice y un punto adicional
  Si se conocen las coordenadas del vértice \( (h, k) \) y de otro punto \( (x_1, y_1) \), se puede usar la forma canónica: $$ y = a(x - h)^2 + k $$ Sustituyendo los valores, se determina el coeficiente \( a \).
• Eje de simetría y dos puntos
  Conociendo la recta de simetría (por ejemplo, \( x = h \)) y dos puntos adicionales, se puede deducir la ecuación general, especialmente útil en forma cuadrática.
• Foco y directriz
  Si se conocen las coordenadas del foco \( (h, k + p) \) y la ecuación de la directriz \( y = k - p \), se puede escribir la ecuación en forma canónica: $$ (x - h)^2 = 4p(y - k) $$ De forma análoga, si la parábola es horizontal y se conoce el foco \( (h + p, k) \) y la directriz \( x = h - p \), se utiliza la forma: $$ (y - k)^2 = 4p(x - h) $$

Y así sucesivamente.