Cómo hallar la ecuación de una parábola conociendo un punto, el eje y la directriz

Para determinar la ecuación de una parábola a partir de un punto \( P(x_0, y_0) \), el eje ($ x=h $ o $ y=k $) y la directriz, sigue estos pasos:

• Si la parábola tiene eje vertical \( x_A = h \), su directriz es una recta horizontal con ecuación \( y_D = k - p \).
  
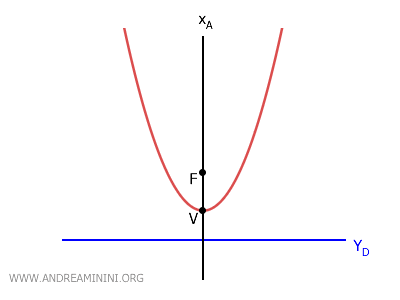
• Si la parábola tiene eje horizontal \( y_A = k \), la directriz es una recta vertical con ecuación \( x_D = h - p \).
  

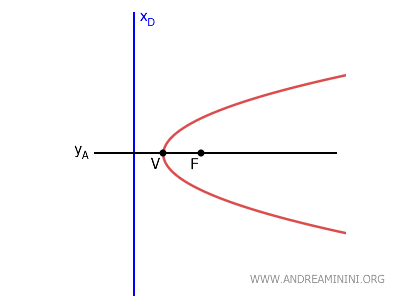
En este contexto, \( (h, k) \) representa el vértice de la parábola y \( p \) es la distancia entre el vértice y el foco.

La ecuación del eje permite determinar si la parábola es vertical u horizontal, lo cual define la forma general de su ecuación.

• Si el eje es vertical \( x=h \), la parábola tiene forma $$ y = ax^2 + bx + c $$ y en su forma canónica $$ (x - h)^2 = 4p(y - k) $$
• Si el eje es horizontal \( y=k \), su forma es $$ x = ay^2 + by + c $$ y en forma estándar $$ (y - k)^2 = 4p(x - h) $$

Conocer las coordenadas del punto y la ecuación de la directriz permite identificar hacia qué lado se abre la parábola.

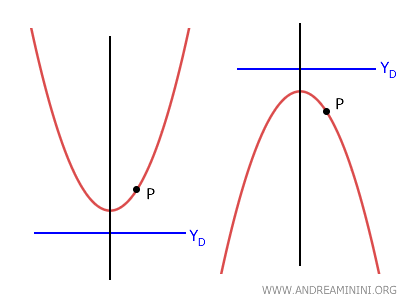
• Si la parábola es vertical y la directriz se encuentra por debajo de la coordenada y del punto \( P \), se abre hacia arriba. Si, en cambio, la directriz está por encima del punto, se abre hacia abajo.
  
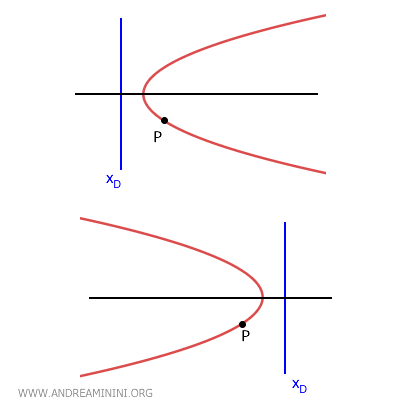
• Si la parábola es horizontal y la directriz está a la izquierda de la coordenada x del punto \( P \), se abre hacia la derecha. Por el contrario, si la directriz está a la derecha, la parábola se abre hacia la izquierda.
  

Finalmente, se sustituyen las coordenadas del punto \( P(x_0, y_0) \) para calcular los parámetros desconocidos.

• Si la parábola tiene eje vertical, se sustituyen \( x_0 \) y \( y_0 \) en la ecuación \( (x_0 - h)^2 = 4p(y_0 - k) \) y se despejan \( h \), \( k \) y \( p \).
• Si tiene eje horizontal, se sustituyen \( x_0 \) y \( y_0 \) en \( (y_0 - k)^2 = 4p(x_0 - h) \) y se resuelven los mismos parámetros.

Ejemplo práctico

Supongamos que se nos da el punto \( P(5, 6) \), la directriz \( y_D = 2 \) y el eje vertical \( x_A = 1 \).

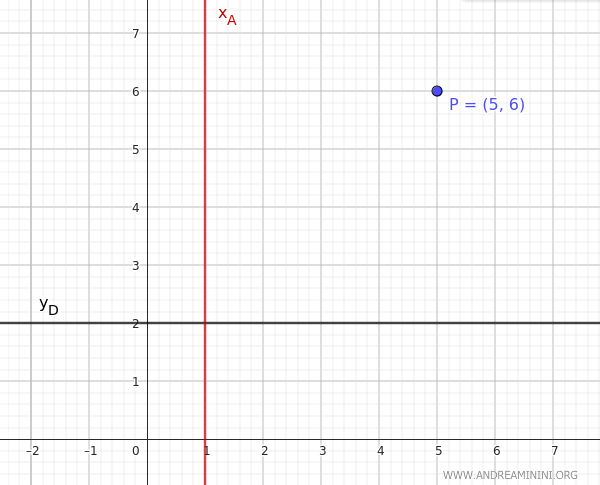
En este caso, la directriz \( y_D=2 \) es horizontal y el eje de simetría \( x_A = 1 \) es vertical, por lo que la parábola también es vertical.

La coordenada y del punto \( P(5,6) \) es \( y_0=6 \), que está por encima de la directriz, lo que indica que la parábola se abre hacia arriba.

Ya que sabemos que es vertical, podemos empezar a construir su ecuación en forma canónica:

$$ (x - h)^2 = 4p(y - k) $$

No conocemos aún el vértice \( V(h,k) \) ni el foco \( F(x_F,y_F) \).

No obstante, tanto el vértice como el foco están alineados sobre el eje \( x_A = 1 \), por lo que comparten la misma coordenada x: \( h = 1 \) y \( x_F = 1 \).

$$ V(h,k) = (1,k) $$

$$ F(x_F,y_F) = (1,y_F) $$

Al sustituir \( h = 1 \) en la ecuación de la parábola, obtenemos:

$$ (x - 1)^2 = 4p(y - k) $$

Sabemos que \( p = y_F - k \), es decir, la distancia entre el foco y el vértice:

$$ p = y_F - k $$

Pero como no conocemos \( y_F \), esa relación no nos ayuda directamente.

En cambio, podemos usar que \( p \) también es igual a la distancia entre el vértice y la directriz:

$$ p = k - y_D $$

$$ p = k - 2 $$

Así, al sustituir \( p = k - 2 \) en la ecuación:

$$ (x - 1)^2 = 4(k - 2)(y - k) $$

Ahora tenemos una única incógnita en la ecuación.

Dado que el punto \( P(5, 6) \) pertenece a la parábola, podemos usarlo para encontrar \( k \). Sustituimos \( x=5 \) y \( y=6 \):

$$ (5 - 1)^2 = 4(k - 2)(6 - k) $$

Lo que nos da:

$$ 16 = 4(k - 2)(6 - k) $$

Dividimos ambos lados entre 4:

$$ 4 = (k - 2)(6 - k) $$

Desarrollamos:

$$ 4 = 6k - k^2 - 12 + 2k $$

$$ -k^2 + 8k - 12 - 4 = 0 $$

$$ -k^2 + 8k - 16 = 0 $$

El discriminante de esta ecuación cuadrática es:

$$ \Delta = b^2 - 4ac = 8^2 - 4 \cdot (-1) \cdot (-16) = 64 - 64 = 0 $$

Como el discriminante es cero, la ecuación tiene una única solución real:

$$ k = \frac{-b \pm \sqrt{\Delta}}{2a} $$

$$ k = \frac{-8 \pm \sqrt{0}}{-2} $$

$$ k = \frac{-8}{-2} = 4 $$

Por lo tanto, el vértice es \( V(h,k) = (1,4) \).

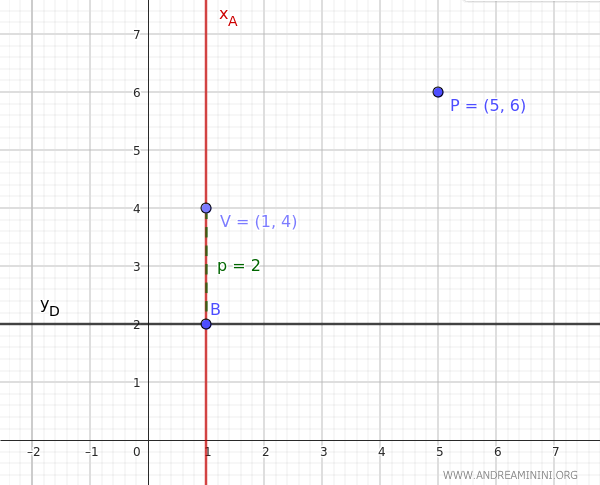
Conociendo \( k \), ahora podemos calcular \( p \):

$$ p = k - y_D = 4 - 2 = 2 $$

Ya tenemos todos los datos necesarios ( h=1, k=4, p=2 ) para escribir la ecuación de la parábola en forma canónica:

$$ (x - h)^2 = 4p(y - k) $$

$$ (x - 1)^2 = 4 \cdot 2 \cdot (y - 4) $$

$$ x^2 - 2x + 1 = 8y - 32 $$

$$ x^2 - 2x + 1 + 32 - 8y = 0 $$

$$ x^2 - 2x - 8y + 33 = 0 $$

Y esta es su representación gráfica:

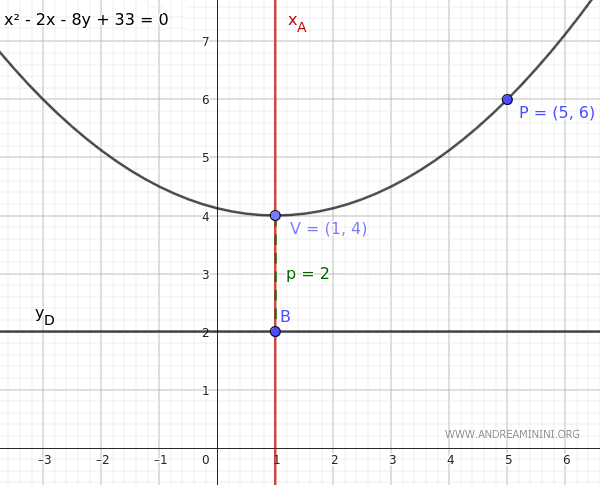
Así es como se obtiene la ecuación buscada.