Segmento parabólico
El segmento parabólico es la región del plano delimitada por un arco de parábola y la cuerda que lo cierra.
Consideremos una recta secante que corta la parábola en los puntos A y B.
El área comprendida entre el arco parabólico AB y la cuerda AB se denomina segmento parabólico.
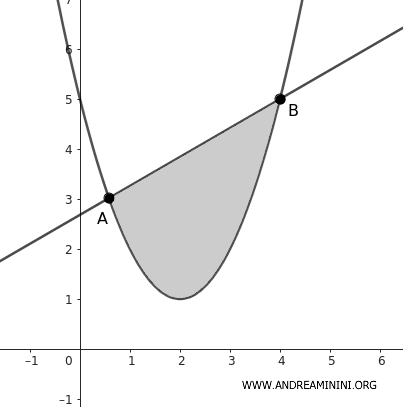
Una propiedad destacada es que el área del segmento parabólico equivale a dos tercios del área del rectángulo ABB'A', construido proyectando los puntos A y B sobre la tangente a la parábola paralela a la cuerda.
$$ A_s = \frac{2}{3} ( \overline{AB} \cdot \overline{AA'} ) $$
Esta propiedad se conoce gracias al teorema de Arquímedes, quien fue el primero en demostrarla en el siglo III a.C.
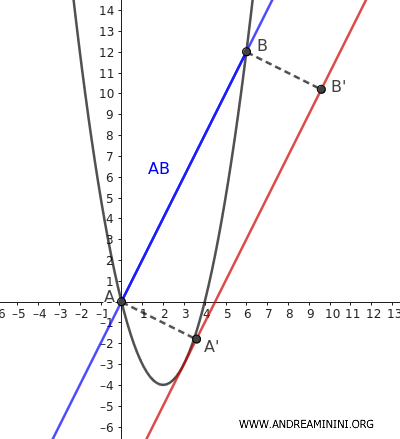
También es posible calcular el área del segmento parabólico mediante técnicas de cálculo integral.
Área del segmento parabólico
La fórmula que permite calcular el área de un segmento parabólico es algo más compleja que la de un círculo.
Si se considera la parábola \( y = ax^2 \) y la cuerda va desde \( x = x_1 \) hasta \( x = x_2 \), con \( x_1 < x_2 \), entonces el área del segmento se obtiene con la siguiente expresión:
$$ A_s = \frac{a}{3} \cdot (x_2^3 - x_1^3) $$
Si la cuerda es simétrica respecto al eje vertical, es decir, va de \( x = -k \) a \( x = k \), la fórmula se simplifica así: $$ A_s = \frac{a}{3} \cdot (k^3 - (-k)^3) $$ $$ A_s = \frac{a}{3} \cdot (k^3 + k^3) = \frac{a}{3} \cdot (2k^3) = \frac{2}{3} \cdot a \cdot k^3 $$
Ejemplo práctico
Consideremos la parábola:
$$ y = x^2 - 4x $$
y la recta secante:
$$ y = 2x $$
Queremos calcular el área del segmento parabólico delimitado por estas dos curvas.
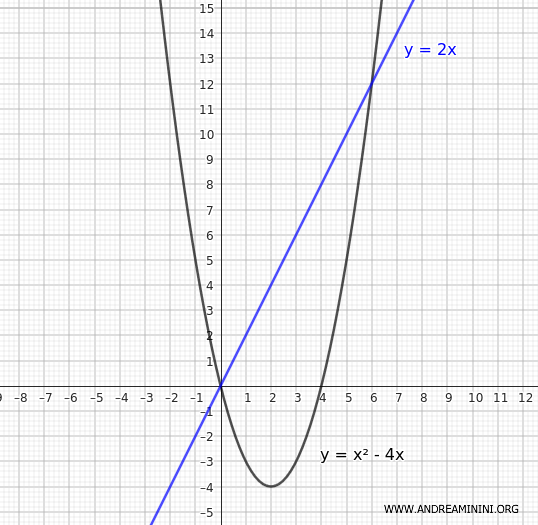
Comenzamos hallando los puntos de intersección, es decir, las soluciones comunes del sistema:
$$ \begin{cases} y = x^2 - 4x \\ y = 2x \end{cases} $$
Sustituyendo:
$$ x^2 - 4x = 2x \Rightarrow x^2 - 6x = 0 \Rightarrow x(x - 6) = 0 $$
De ahí se obtiene: $$ x_1 = 0, \quad x_2 = 6 $$
Calculamos las correspondientes coordenadas \( y \) usando la ecuación de la recta:
$$ y_1 = 2 \cdot 0 = 0, \quad y_2 = 2 \cdot 6 = 12 $$
Por lo tanto, los puntos de intersección son: A(0, 0) y B(6, 12)
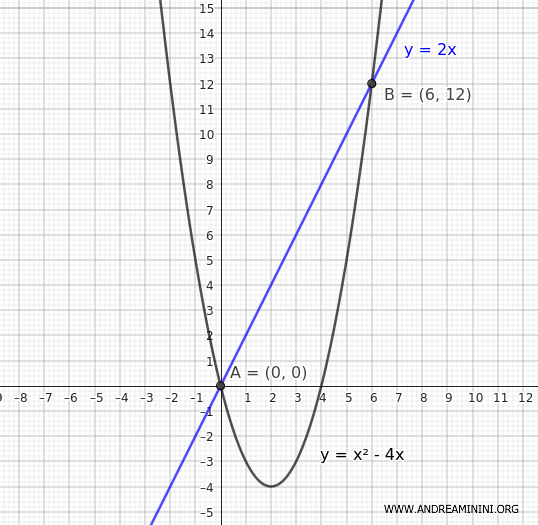
Ahora calculamos la longitud de la cuerda AB:
$$ \overline{AB} = \sqrt{(x_2 - x_1)^2 + (y_2 - y_1)^2} = \sqrt{6^2 + 12^2} = \sqrt{36 + 144} = \sqrt{180} $$
$$ \overline{AB} = \sqrt{2^2 \cdot 3^2 \cdot 5} = 6 \cdot \sqrt{5} $$
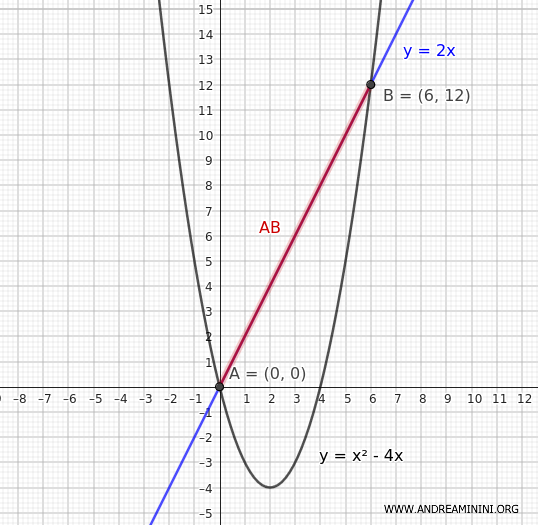
Buscamos ahora la recta paralela a \( y = 2x \) que sea tangente a la parábola \( y = x^2 - 4x \).
Sea \( y = 2x + q \) la ecuación de dicha recta. La condición de tangencia se obtiene igualando las expresiones e imponiendo que el discriminante sea cero:
$$ x^2 - 6x - q = 0 $$
El discriminante es:
$$ \Delta = (-6)^2 - 4(1)(-q) = 36 + 4q = 0 \Rightarrow q = -9 $$
Así, la recta tangente es: $$ y = 2x - 9 $$
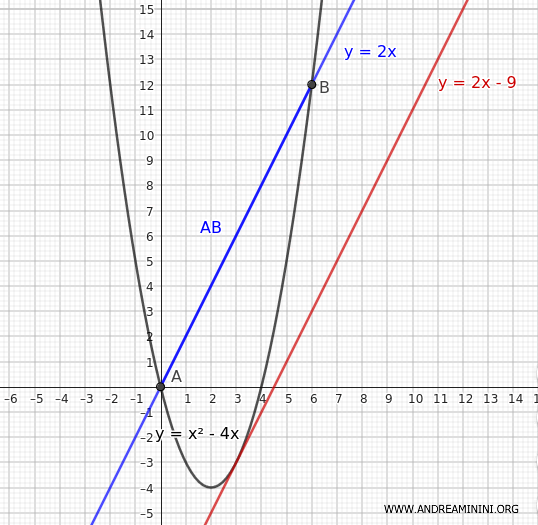
Calculamos ahora la distancia entre las dos rectas paralelas:
$$ d = \frac{|c_2 - c_1|}{\sqrt{1 + m^2}} = \frac{|-9 - 0|}{\sqrt{1 + 4}} = \frac{9}{\sqrt{5}} $$
Verificación. Tomando un punto sobre la recta \( y = 2x \), por ejemplo \( P(0, 0) \), su distancia a la recta paralela \( y = 2x - 9 \) se calcula con: $$ d = \frac{|a x_0 + b y_0 + c|}{\sqrt{a^2 + b^2}} $$ donde \( a = -2 \), \( b = 1 \), \( c = 9 \): $$ d = \frac{|0 + 0 + 9|}{\sqrt{1^2 + (-2)^2}} = \frac{9}{\sqrt{5}} $$
Por tanto, la distancia entre las dos rectas es \( \overline{AA'} = \overline{BB'} = \frac{9}{\sqrt{5}} \)
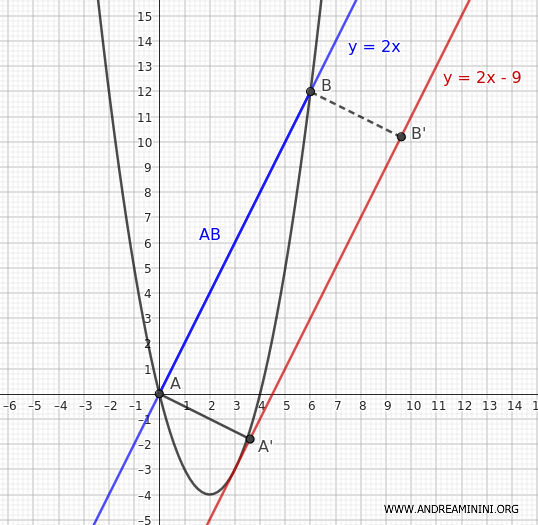
Ya conocemos la base \( \overline{AB} = 6 \cdot \sqrt{5} \) y la altura \( \overline{AA'} = \frac{9}{\sqrt{5}} \) del rectángulo ABB'A'.
El área del segmento parabólico será entonces:
$$ A_s = \frac{2}{3} \cdot (6 \cdot \sqrt{5}) \cdot \left( \frac{9}{\sqrt{5}} \right) = \frac{2}{3} \cdot 54 = 36 $$
Por lo tanto, el área del segmento parabólico es 36.
Solución alternativa
Este mismo problema también puede resolverse utilizando la siguiente fórmula:
$$ A_s = \frac{a}{3} \cdot (x_2^3 - x_1^3) $$
donde \( x_1 \) y \( x_2 \) representan las abscisas de los puntos de intersección entre la cuerda y la parábola.
Consideremos la parábola:
$$ y = x^2 - 4x $$
y la recta secante:
$$ y = 2x $$
Como ya se vio en el ejemplo anterior, los puntos de intersección son A(x1, y1) = (0, 0) y B(x2, y2) = (6, 12).
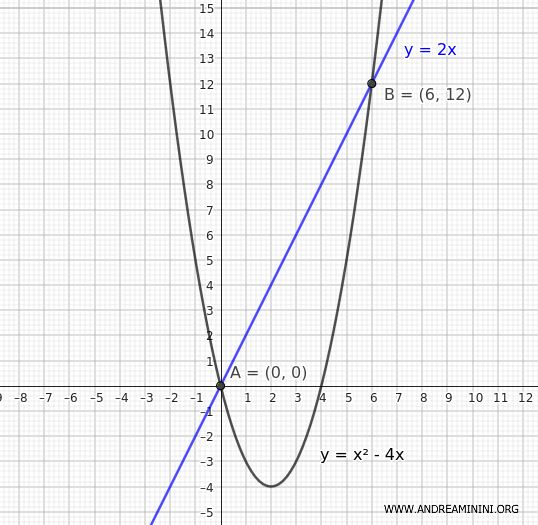
Aplicamos la fórmula con \( x_1 = 0 \) y \( x_2 = 6 \):
$$ A_s = \frac{a}{3} \cdot (6^3 - 0^3) = \frac{a}{3} \cdot 216 $$
Como en este caso \( a = 1 \), se obtiene:
$$ A_s = \frac{1}{3} \cdot 216 = 72 $$
Nota: Esta fórmula es válida únicamente cuando la parábola tiene forma canónica \( y = ax^2 \) y está orientada con el vértice sobre el eje y. En este ejemplo, la parábola es de la forma \( y = ax^2 + bx + c \), por lo que el resultado de 72 no corresponde con el área real del segmento, que es 36. La fórmula anterior debe aplicarse con precaución.
Cálculo del área del segmento parabólico mediante integrales
Otra forma de determinar el área del segmento parabólico es a través del cálculo integral.
El área del segmento se obtiene como la diferencia entre el área del trapecio ABCD, definido por la cuerda AB y el eje x, y la integral de la parábola entre los puntos \( x_1 \) y \( x_2 \): $$ \text{Área (segmento)} = \text{Área (ABCD)} - \int_{x_1}^{x_2} (ax^2 + bx + c) \, dx $$ 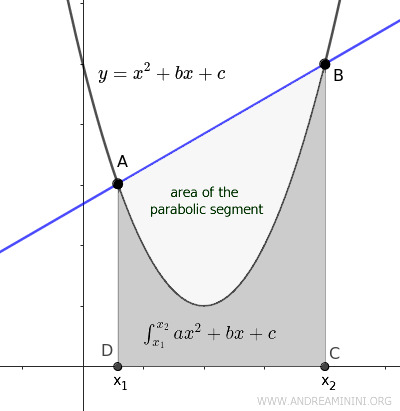
En términos generales, la integral de una parábola permite calcular el área entre la curva y el eje x siempre que la parábola esté contenida en la región positiva del eje y.
En consecuencia, el área del segmento parabólico puede obtenerse restando el área bajo la curva al área del trapecio definido por la cuerda y el eje horizontal.
Nota: Esta metodología sigue siendo válida incluso cuando la parábola se extiende por debajo del eje x. En estos casos, la integral definida calcula la diferencia neta entre las áreas por encima y por debajo del eje, y por tanto no representa el área geométrica total. A continuación, se analiza un ejemplo concreto.
Ejemplo
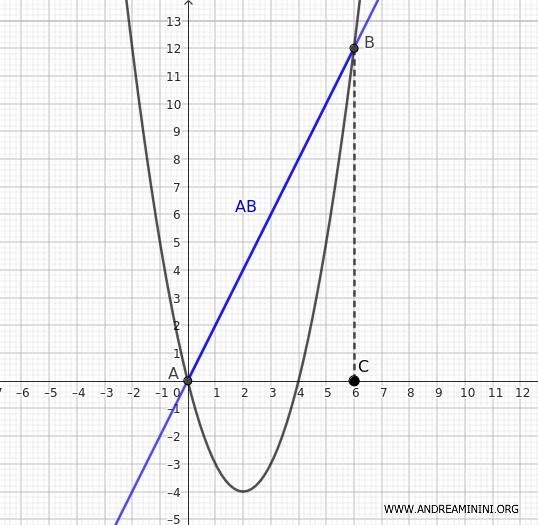
Analicemos nuevamente la parábola \( y = x^2 - 4x \) y la recta \( y = 2x \), que se intersectan en los puntos A(0, 0) y B(6, 12).
Determinaremos el área del segmento parabólico como la diferencia entre el área del trapecio y el área bajo la parábola.
1] Cálculo del área del trapecio
El área del trapecio \( A_{\text{trapecio}} \) se obtiene como el promedio de las longitudes de sus bases multiplicado por la altura:
$$ A_{\text{trapecio}} = \frac{(b_1 + b_2) \cdot h}{2} $$
En este caso, \( b_1 = y_1 = 0 \), \( b_2 = y_2 = 12 \), y \( h = x_2 - x_1 = 6 \):
$$ A_{\text{trapecio}} = \frac{(0 + 12) \cdot 6}{2} = 36 $$
Así, el área del trapecio es 36 unidades cuadradas.
Obsérvese que, en este caso particular, el trapecio coincide con el triángulo ABC.
2] Cálculo del área bajo la parábola
Integramos la función \( y = x^2 - 4x \) en el intervalo \( [0, 6] \):
\[ A_{\text{parábola}} = \int_{0}^{6} (x^2 - 4x) \, dx = \int_0^6 x^2 \, dx - \int_0^6 4x \, dx \]
Las primitivas respectivas son:
\[ \int x^2 dx = \frac{x^3}{3}, \qquad \int 4x dx = 2x^2 \]
Evaluando entre los límites dados:
\[ \left[ \frac{x^3}{3} \right]_0^6 = \frac{6^3}{3} - 0 = 72 \]
\[ \left[ 2x^2 \right]_0^6 = 2 \cdot 36 = 72 \]
Por tanto, el área neta bajo la curva es:
\[ A_{\text{parábola}} = 72 - 72 = 0 \]
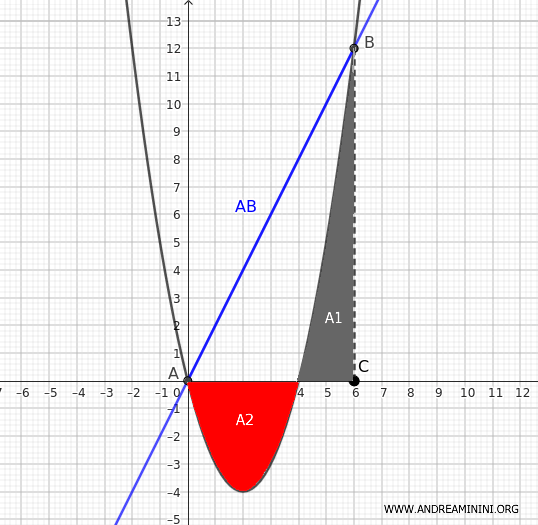
Nota: En el caso de una parábola que cruza el eje x, la integral definida mide la diferencia entre las áreas positivas y negativas. Es decir, el área por encima del eje x se suma, y la que está por debajo se resta. De ahí que el valor de la integral pueda anularse, como ocurre en este ejemplo, aunque geométricamente exista un área no nula entre las curvas.
3] Cálculo del área del segmento parabólico
Finalmente, obtenemos el área del segmento como:
$$ \text{Área (segmento)} = \text{Área (ABCD)} - \int_{x_1}^{x_2} (ax^2 + bx + c) \, dx $$
$$ \text{Área (segmento)} = 36 - 0 = 36 $$
Por lo tanto, el área del segmento parabólico es igual a \( 36 \).
Y así sucesivamente.