Cómo determinar la ecuación de una parábola a partir del vértice y la directriz

Para encontrar la ecuación de una parábola cuyo eje de simetría es paralelo al eje y, conociendo las coordenadas del vértice $ V(h; k) $ y la ecuación de la directriz $ y_d $, se utiliza la forma estándar de la parábola: $$ (x - h)^2 = 4p(y - k) $$ donde $ p = |k - y_d| $ representa la distancia entre el vértice y la directriz.

Cuando el eje de simetría es vertical, la directriz es una recta horizontal, ya que siempre es perpendicular a dicho eje.

El foco se encuentra en la dirección opuesta a la directriz respecto al vértice. Por tanto, la distancia entre el vértice $ V(h,k) $ y la directriz $ |k - y_d| $ coincide con la distancia entre el vértice y el foco $ F $.

En estos casos, la parábola adopta la forma:

$$ (x - h)^2 = 4p(y - k) $$

El signo de $ p $ depende de la posición del vértice con respecto a la directriz:

Si $ k > y_d $, la parábola se abre hacia arriba y $ p $ es positivo.
Si $ k < y_d $, se abre hacia abajo y $ p $ es negativo.

Nota: Este procedimiento puede adaptarse a otros casos. Por ejemplo, si la directriz es vertical, la parábola tendrá eje horizontal y su ecuación será de la forma $ (y - k)^2 = 4p(x - h) $.

Ejemplo práctico

Supongamos que el vértice es $ V(3, 2) $ y la directriz está dada por $ y = -1 $.

La distancia entre la ordenada del vértice $ k = 2 $ y la directriz $ y = -1 $ es:

$$ p = |2 - (-1)| = 3 $$

Una vez determinada esta distancia, es necesario establecer si la parábola se abre hacia arriba o hacia abajo para asignar el signo correcto a $ p $.

Como $ 2 > -1 $, la parábola se abre hacia arriba, por lo que $ p $ es positivo:

$$ p = 3 $$

Ahora sustituimos los valores conocidos en la ecuación estándar:

$$ (x - h)^2 = 4p(y - k) $$

Con $ p = 3 $, $ h = 3 $ y $ k = 2 $, obtenemos:

$$ (x - 3)^2 = 4 \cdot 3 \cdot (y - 2) $$

Desarrollamos ambos miembros:

$$ x^2 - 6x + 9 = 12y - 24 $$

$$ 12y = x^2 - 6x + 33 $$

$$ y = \frac{x^2}{12} - \frac{x}{2} + \frac{33}{12} $$

Por tanto, la ecuación de la parábola con vértice en $ (3, 2) $ y directriz $ y = -1 $ es:

$$ y = \frac{x^2}{12} - \frac{x}{2} + \frac{33}{12} $$

Como el foco se sitúa a la misma distancia $ p = 3 $ del vértice, pero en dirección opuesta a la directriz, sus coordenadas son: $ F(h, k + p) = (3, 5) $.

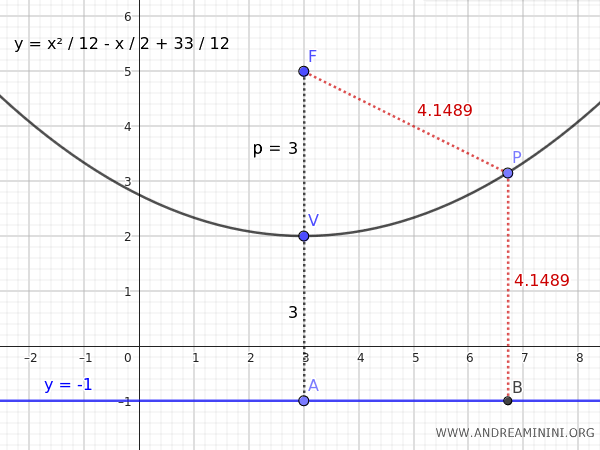
the graph of the parabola

Para cualquier punto $ P $ sobre la parábola, se cumple que su distancia al foco $ F(3, 5) $ es igual a su distancia a la directriz $ y_d = -1 $:

$$ \overline{PF} = \overline{PB} $$