Cómo obtener la ecuación de una parábola a partir de dos puntos y el eje
Si se conocen dos puntos distintos \((x_1, y_1)\) y \((x_2, y_2)\), junto con la ecuación del eje de simetría \( x = h \) de una parábola, es posible determinar su ecuación siguiendo estos pasos:
- Una parábola cuyo eje es paralelo al eje y tiene la forma $$ y = a(x - h)^2 + k $$, donde \( (h, k) \) es el vértice de la parábola.
- Sustituimos los dos puntos conocidos en la ecuación de la parábola: $$ y_1 = a(x_1 - h)^2 + k $$ $$ y_2 = a(x_2 - h)^2 + k $$ siendo \( (h,k) \) las coordenadas del vértice.
- Esto nos da un sistema de dos ecuaciones con dos incógnitas (\( a \) y \( k \)). Al resolverlo, obtenemos los valores de \( a \) y \( k \), con lo cual completamos la ecuación de la parábola.
Método alternativo. Si los puntos \((x_1, y_1)\) y \((x_2, y_2)\) no son simétricos respecto al eje \( x=h \), se puede hallar un tercer punto \((x_3, y_3)\) simétrico respecto a uno de los anteriores y deducir la ecuación de la parábola a partir de tres puntos.
Ejemplo práctico
Dados los puntos \((2, 3)\) y \((3,5)\), y el eje de simetría \( x = 1 \) de una parábola, se desea encontrar su ecuación.
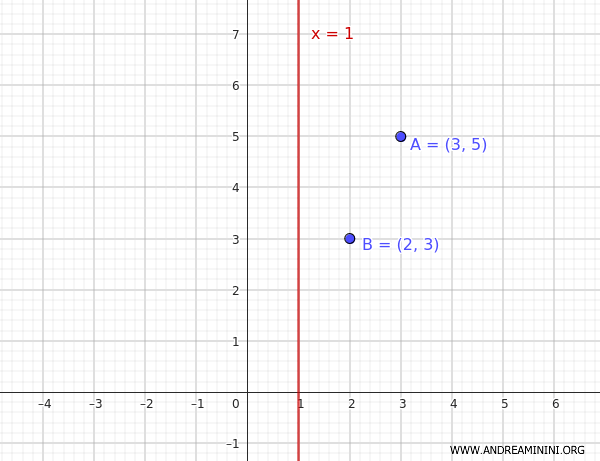
La forma general de una parábola con eje paralelo al eje y es:
$$ y = a(x - h)^2 + k $$
donde \( (h,k) \) representa el vértice \( V \) de la parábola.
En este caso, el eje de simetría es \( x=1 \), lo que implica que \( h = 1 \), ya que el vértice \( V(h,k) = (1,k) \) debe estar sobre dicho eje.
$$ y = a(x - 1)^2 + k $$
Sustituimos las coordenadas de los dos puntos conocidos \((x_1,y_1)=(2, 3)\) y \((x_2,y_2)=(3, 5)\) en la ecuación general:
$$ \begin{cases} y_1 = a(x_1 - 1)^2 + k \\ \\ y_2 = a(x_2 - 1)^2 + k \end{cases} $$
$$ \begin{cases} 3 = a(2 - 1)^2 + k \\ \\ 5 = a(3 - 1)^2 + k \end{cases} $$
$$ \begin{cases} 3 = a(1)^2 + k \\ \\ 5 = a(2)^2 + k \end{cases} $$
$$ \begin{cases} 3 = a + k \\ \\ 5 = 4a + k \end{cases} $$
Este sistema de ecuaciones tiene dos incógnitas.
Procedemos a resolverlo por sustitución para hallar los valores de \( a \) y \( k \):
$$ \begin{cases} k = 3 - a \\ \\ 5 = 4a + k \end{cases} $$
$$ \begin{cases} k = 3 - a \\ \\ 5 = 4a + (3 - a) \end{cases} $$
$$ \begin{cases} k = 3 - a \\ \\ 5 = 3a + 3 \end{cases} $$
$$ \begin{cases} k = 3 - a \\ \\ 3a = 2 \end{cases} $$
$$ \begin{cases} k = 3 - a \\ \\ a = \frac{2}{3} \end{cases} $$
$$ \begin{cases} k = 3 - \frac{2}{3} \\ \\ a = \frac{2}{3} \end{cases} $$
$$ \begin{cases} k = \frac{7}{3} \\ \\ a = \frac{2}{3} \end{cases} $$
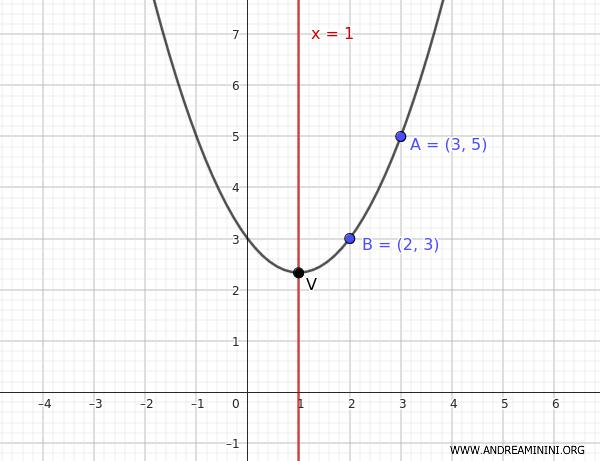
Ya que conocemos \( a \) y \( k \), el vértice tiene coordenadas \( (h,k) = (1, \frac{7}{3}) \).
Con estos valores, escribimos la ecuación de la parábola:
$$ y = a(x - h)^2 + k $$
$$ y = \frac{2}{3} \cdot (x - 1)^2 + \frac{7}{3} $$
A continuación se muestra su representación gráfica:
Solución alternativa
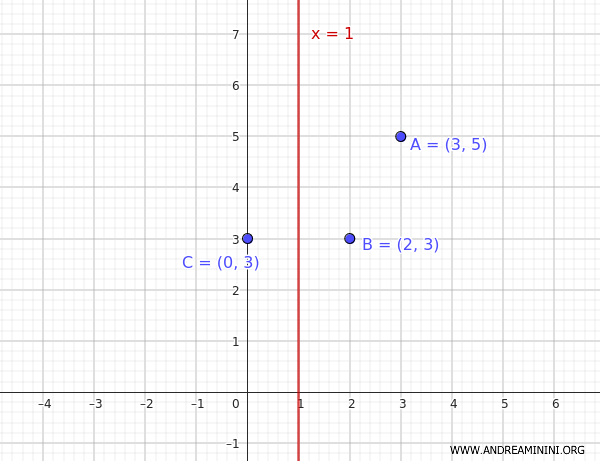
Conocemos las coordenadas de dos puntos \( (2, 3)\) y \((3,5)\), así como el eje de simetría \( x = 1 \) de la parábola.

Estos dos puntos no son simétricos entre sí respecto al eje \( x = 1 \).
Elegimos uno de ellos, por ejemplo \( B(2,3) \), y calculamos el punto \( C(0,3) \), que es simétrico respecto a dicho eje.
Cuando el eje de simetría es vertical, según la simetría axial, un punto es simétrico de otro si se cumple:
$$ \begin{cases} x' = 2h - x \\ \\ y' = y \end{cases} $$
En este caso, el eje es \( h = 1 \), y las coordenadas del punto \( B \) son \( x = 2 \) y \( y = 3 \).
$$ \begin{cases} x' = 2 \cdot 1 - 2 \\ \\ y' = 3 \end{cases} $$
$$ \begin{cases} x' = 0 \\ \\ y' = 3 \end{cases} $$
Por lo tanto, el tercer punto simétrico es \( C(0,3) \).
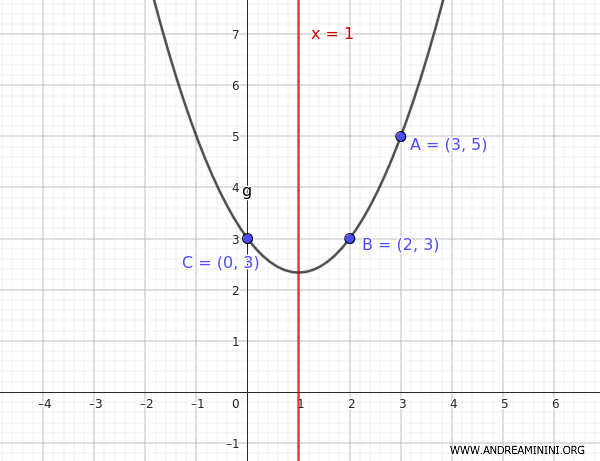
Con los puntos \( A(3,5) \), \( B(2,3) \) y \( C(0,3) \), podemos plantear un sistema de tres ecuaciones:
$$ \begin{cases} ax_1^2 + bx_1 + c = y_1 \\ \\ ax_2^2 + bx_2 + c = y_2 \\ \\ ax_3^2 + bx_3 + c = y_3 \end{cases} $$
Sustituimos las coordenadas de los puntos en las ecuaciones:
$$ \begin{cases} a \cdot 3^2 + b \cdot 3 + c = 5 \\ \\ a \cdot 2^2 + b \cdot 2 + c = 3 \\ \\ a \cdot 0^2 + b \cdot 0 + c = 3 \end{cases} $$
$$ \begin{cases} 9a + 3b + c = 5 \\ \\ 4a + 2b + c = 3 \\ \\ c = 3 \end{cases} $$
Resolvemos el sistema para hallar los coeficientes \( a \), \( b \) y \( c \):
$$ \begin{cases} 9a + 3b + 3 = 5 \\ \\ 4a + 2b + 3 = 3 \\ \\ c = 3 \end{cases} $$
$$ \begin{cases} 9a + 3b = 2 \\ \\ 4a + 2b = 0 \\ \\ c = 3 \end{cases} $$
$$ \begin{cases} 9a + 3b = 2 \\ \\ b = \frac{-4a}{2} \\ \\ c = 3 \end{cases} $$
$$ \begin{cases} 9a + 3b = 2 \\ \\ b = -2a \\ \\ c = 3 \end{cases} $$
$$ \begin{cases} 9a + 3(-2a) = 2 \\ \\ b = -2a \\ \\ c = 3 \end{cases} $$
$$ \begin{cases} 9a - 6a = 2 \\ \\ b = -2a \\ \\ c = 3 \end{cases} $$
$$ \begin{cases} 3a = 2 \\ \\ b = -2a \\ \\ c = 3 \end{cases} $$
$$ \begin{cases} a = \frac{2}{3} \\ \\ b = -2a \\ \\ c = 3 \end{cases} $$
$$ \begin{cases} a = \frac{2}{3} \\ \\ b = -2 \cdot \frac{2}{3} \\ \\ c = 3 \end{cases} $$
$$ \begin{cases} a = \frac{2}{3} \\ \\ b = -\frac{4}{3} \\ \\ c = 3 \end{cases} $$
Ya tenemos los coeficientes \( a \), \( b \) y \( c \), con los cuales escribimos la ecuación de la parábola:
$$ y = ax^2 + bx + c $$
$$ y = \frac{2}{3} x^2 - \frac{4}{3}x + 3 $$
Esta es la ecuación que representa la parábola buscada.
Y así sucesivamente.