Cómo obtener la ecuación de una parábola a partir de un punto y la directriz

Para deducir la ecuación de una parábola conociendo las coordenadas del foco \((h, k)\) y la ecuación de la directriz \(y = d\) o \(x = d\), puedes seguir los siguientes pasos:

• Si la directriz es horizontal \(y = d\)
  La ecuación de la parábola se determina del siguiente modo:
  1. La distancia desde un punto arbitrario \((x, y)\) al foco es: $$ \sqrt{(x - h)^2 + (y - k)^2} $$
  2. La distancia desde ese mismo punto a la directriz es: $$ |y - d| $$
  3. Como una parábola está definida como el conjunto de puntos equidistantes del foco y de la directriz, igualamos ambas expresiones: $$ \sqrt{(x - h)^2 + (y - k)^2} = |y - d| $$ Elevando al cuadrado ambos miembros: $$ (x - h)^2 + (y - k)^2 = (y - d)^2 $$ Desarrollando y simplificando se obtiene la forma estándar de la parábola.
• Si la directriz es vertical \(x = d\)
  En este caso, el procedimiento es análogo:
  1. La distancia de un punto genérico \((x, y)\) al foco es: $$ \sqrt{(x - h)^2 + (y - k)^2} $$
  2. La distancia del mismo punto a la directriz es: $$ |x - d| $$
  3. Igualando ambas expresiones, se obtiene: $$ \sqrt{(x - h)^2 + (y - k)^2} = |x - d| $$ Elevando al cuadrado: $$ (x - h)^2 + (y - k)^2 = (x - d)^2 $$ Al desarrollar y simplificar se obtiene la ecuación canónica de la parábola.

Ejemplo práctico

En este caso, el foco está en \( F(2, 3) \) y la directriz es \( y = 1 \).

Dado que la directriz es horizontal, el eje de simetría de la parábola es vertical (paralelo al eje y).

Según la definición, la distancia desde cualquier punto \( P(x, y) \) de la parábola al foco \( F(2, 3) \) debe coincidir con su distancia a la directriz \( y = 1 \):

$$ \sqrt{(x - 2)^2 + (y - 3)^2} = |y - 1| $$

Elevando ambos miembros al cuadrado:

$$ \left( \sqrt{(x - 2)^2 + (y - 3)^2} \right)^2 = \left( |y - 1| \right)^2 $$

$$ (x - 2)^2 + (y - 3)^2 = (y - 1)^2 $$

Desarrollamos ambos lados:

$$ x^2 - 4x + 4 + y^2 - 6y + 9 = y^2 - 2y + 1 $$

Eliminamos \( y^2 \) en ambos miembros y agrupamos términos:

$$ x^2 - 4x + 13 = -2y + 1 + 6y $$

$$ x^2 - 4x + 12 = 4y $$

Despejamos \( y \):

$$ y = \frac{x^2}{4} - x + 3 $$

Esta es la ecuación de la parábola con foco en \( (2, 3) \) y directriz \( y = 1 \).

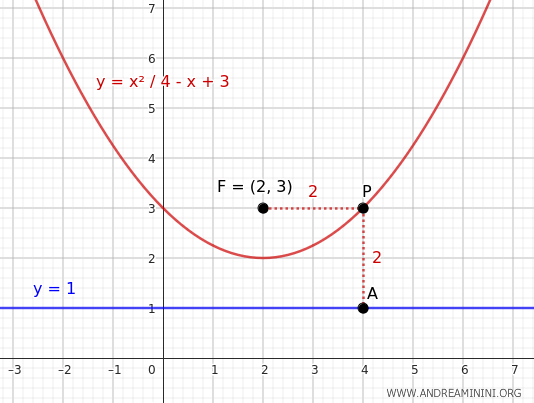
Así, podemos deducir la ecuación de una parábola a partir de las coordenadas del foco y la ecuación de la directriz.

Y así sucesivamente.