Teorema de Arquímedes sobre el Área de un Segmento Parabólico
El área \( S \) de un segmento parabólico - es decir, la región delimitada por una parábola y una cuerda AB que no coincide con su eje de simetría - equivale a dos tercios del área \( A \) del rectángulo construido sobre la tangente a la parábola paralela a dicha cuerda. $$ S = \frac{2}{3} \times A $$
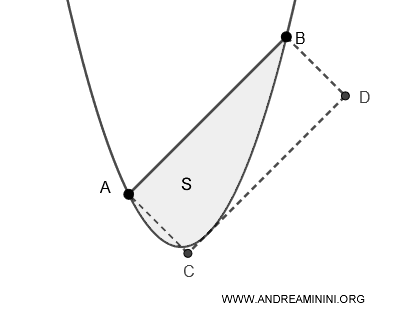
Otra forma de expresar esta área consiste en afirmar que equivale a cuatro tercios del área del triángulo inscrito ABC, donde la base es la cuerda AB y el vértice opuesto C corresponde al punto de tangencia entre la parábola y la recta paralela a AB.
Si el área del triángulo inscrito es \( A \), entonces el área \( S \) del segmento parabólico se calcula como:
$$ S = \frac{4}{3} \times A $$
Esta fórmula resulta sorprendentemente precisa para su época y pone de manifiesto la brillantez de los métodos geométricos de Arquímedes.
Nota: Para obtener el área exacta de un segmento parabólico, lo habitual sería integrar la función que define la parábola. Sin embargo, el teorema de Arquímedes proporciona un método numérico alternativo que no requiere el uso del cálculo integral.
Ejemplo práctico
Consideremos la parábola:
$$ y = x^2 $$
Tomamos una cuerda AB cuyos extremos son A(-1, 1) y B(2, 4).
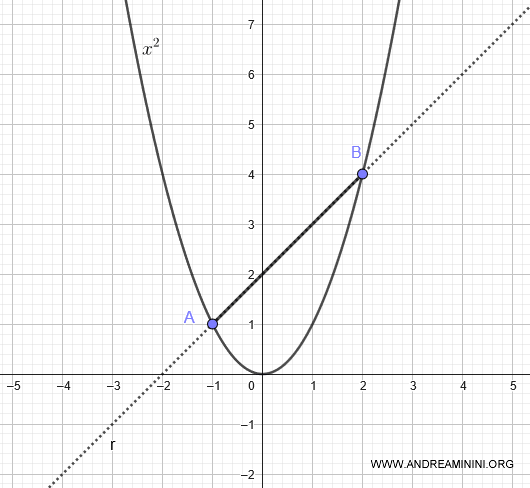
Queremos calcular el área encerrada entre la parábola y la cuerda AB.
Aplicaremos el método de Arquímedes. El primer paso consiste en hallar la recta tangente a la parábola que sea paralela a la cuerda AB.
La cuerda AB está contenida en la recta r:
$$ y = x + 2 $$
El conjunto de rectas paralelas a r está dado por:
$$ y = mx + q $$
Los puntos de intersección entre la parábola \( y = x^2 \) y la familia de rectas \( y = mx + q \) se obtienen resolviendo:
$$ x^2 = mx + q $$
Nos interesa el caso en que la recta sea tangente a la parábola.
Reescribimos la ecuación en forma general:
$$ y - mx - q = 0 $$
Para que haya tangencia, el discriminante debe anularse:
$$ \Delta = 0 $$
El discriminante es:
$$ \Delta = b^2 - 4ac = 0 $$
En nuestro caso, con \( a = 1 \), \( b = -m \) y \( c = -q \), se tiene:
$$ \Delta = (-m)^2 - 4 \cdot 1 \cdot (-q) = 0 $$
$$ m^2 + 4q = 0 $$
Despejamos \( q \):
$$ q = - \frac{m^2}{4} $$
Por tanto, la recta tangente buscada es:
$$ y = mx - \frac{m^2}{4} $$
La pendiente \( m \) de la recta que pasa por A y B, \( y = x + 2 \), es \( m = 1 \).
Entonces, la recta tangente es:
$$ y = x - \frac{1}{4} $$
Esta es la ecuación de la tangente a la parábola \( y = x^2 \), paralela a la cuerda AB.
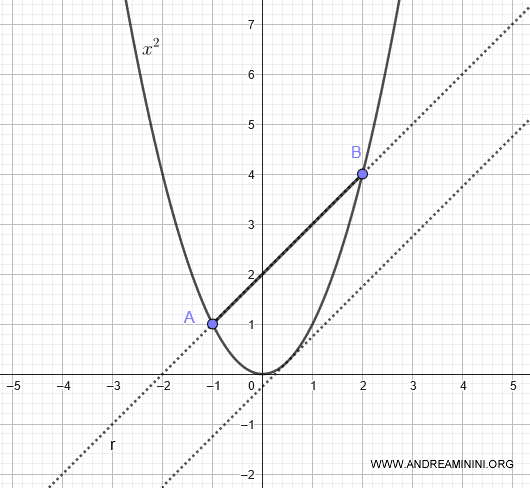
Desde los puntos A y B trazamos perpendiculares hasta la tangente, formando así el rectángulo ABCD.
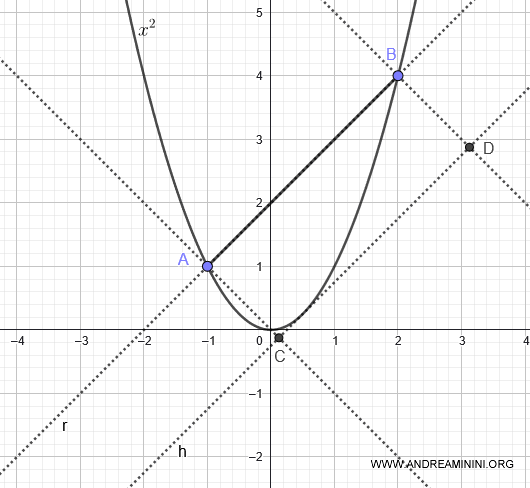
Según el teorema de Arquímedes, el área encerrada entre la parábola y la cuerda AB equivale a dos tercios del área del rectángulo ABCD.
Calculamos la longitud del lado AB utilizando la fórmula de distancia:
$$ \overline{AB} = \sqrt{(x_B - x_A)^2 + (y_B - y_A)^2} $$
Con \( A(-1, 1) \) y \( B(2, 4) \):
$$ \overline{AB} = \sqrt{(2 + 1)^2 + (4 - 1)^2} = \sqrt{9 + 9} = \sqrt{18} $$
Para hallar la altura del rectángulo (lado AC), usamos la fórmula de distancia punto-recta:
$$ \overline{AC} = \frac{|-x + y + \frac{1}{4}|}{\sqrt{2}} $$
En el punto A(-1, 1):
$$ \overline{AC} = \frac{|1 + 1 + \frac{1}{4}|}{\sqrt{2}} = \frac{\frac{9}{4}}{\sqrt{2}} = \frac{9}{4 \cdot \sqrt{2}} $$
Calculamos ahora el área del rectángulo ABCD:
$$ A = \overline{AB} \cdot \overline{AC} = \sqrt{18} \cdot \frac{9}{4 \cdot \sqrt{2}} = 3 \cdot \frac{9}{4} = \frac{27}{4} $$
Según el teorema de Arquímedes:
$$ S = \frac{2}{3} \cdot \frac{27}{4} = \frac{27}{6} \approx 4.5 $$
Por tanto, el área encerrada entre la parábola y la cuerda AB es 4.5.
Verificación: Para verificar este resultado, calculamos el área entre la cuerda AB y el eje x.
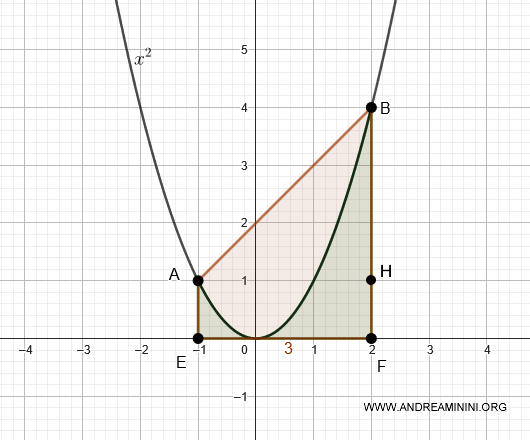
La región AEFB está formada por el triángulo AHF (base y altura de 3) y el rectángulo AEFH (base 3, altura 1):
$$ Área(AEFB) = \frac{3 \cdot 3}{2} + 3 \cdot 1 = \frac{9}{2} + 3 = \frac{15}{2} = 7.5 $$
El área bajo la parábola se obtiene integrando \( x^2 \) de \( x = -1 \) a \( x = 2 \):
$$ \int_{-1}^2 x^2 \, dx = \left[ \frac{x^3}{3} \right]_{-1}^2 = \frac{8}{3} + \frac{1}{3} = 3 $$
Entonces, el área del segmento es:
$$ S = 7.5 - 3 = 4.5 $$
Este valor coincide con el obtenido mediante el método de Arquímedes.
Demostración
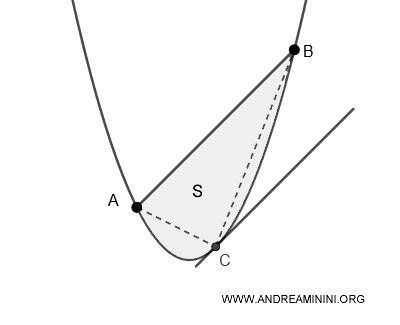
Sea un segmento parabólico, definido como la región delimitada por una parábola y una cuerda AB que conecta dos puntos de la curva.
Construimos el triángulo inscrito ABC, tomando AB como base y el vértice C en la parábola, sobre la perpendicular trazada desde el punto medio M de AB.
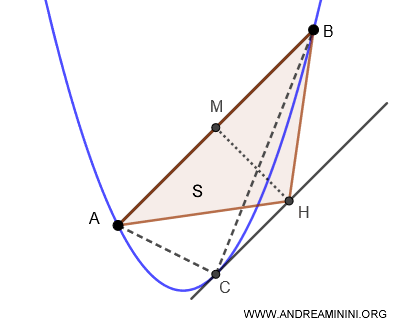
Para demostrar su resultado, Arquímedes empleó un procedimiento que hoy llamaríamos "método de exhaución", antecesor del cálculo integral.
Dividió el segmento en una sucesión infinita de triángulos, demostrando que la suma de sus áreas converge al área real del segmento parabólico.
Y así sucesivamente.