Recta tangente, secante o exterior a una parábola

Una recta puede ser tangente, secante o exterior a una parábola dependiendo de si la corta en un punto, en dos puntos o si no la corta en absoluto.

Para determinar los puntos de intersección, es necesario resolver una ecuación cuadrática.

$$ ax^2+x \cdot (b-m)+c-q=0 $$

Donde \( a \), \( b \) y \( c \) son los coeficientes de la parábola \( y = ax^2 + bx + c \), y \( m \) y \( q \) representan respectivamente la pendiente y la ordenada al origen de la recta \( y = mx + q \).

El número de soluciones reales de la ecuación depende del valor del discriminante \( \Delta = b^2 - 4ac \):

• Si \( \Delta = 0 \), la recta es tangente a la parábola, ya que la ecuación tiene una única solución real, lo que indica que ambas curvas se tocan en un solo punto.
  
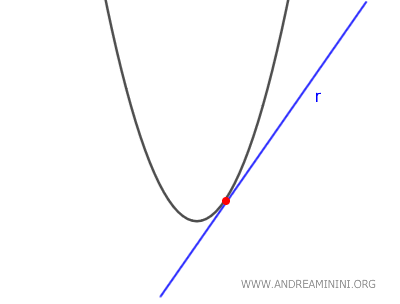
• Si \( \Delta > 0 \), la recta es secante, porque la ecuación tiene dos soluciones reales distintas: la recta corta a la parábola en dos puntos diferentes.
  
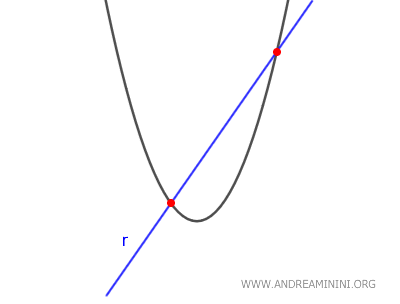
• Si \( \Delta < 0 \), la recta es exterior, ya que la ecuación no tiene soluciones reales: la recta no llega a interceptar la parábola.
  

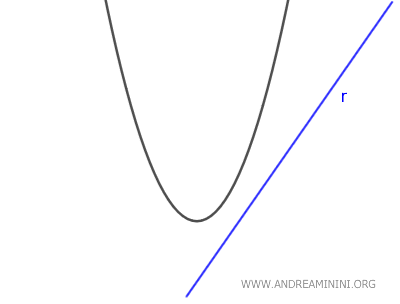
Nota: Este criterio solo se aplica si la recta no es vertical (es decir, no paralela al eje \( y \)), ya que en ese caso no puede expresarse mediante la ecuación explícita \( y = mx + q \).

Ejemplo práctico

Veamos un ejemplo concreto. Consideramos la parábola:

$$ y = x^2 + 2x - 1 $$

y la recta:

$$ y = 4x - 2 $$

Queremos determinar si la recta es tangente, secante o exterior respecto a la parábola.

Igualamos ambas expresiones para hallar los posibles puntos de intersección:

$$ x^2 + 2x - 1 = 4x - 2 $$

$$ x^2 + 2x - 1 - 4x + 2 = 0 $$

$$ x^2 - 2x + 1 = 0 $$

Calculamos ahora el discriminante:

$$ \Delta = b^2 - 4ac $$

Con \( a = 1 \), \( b = -2 \), \( c = 1 \):

$$ \Delta = (-2)^2 - 4 \cdot 1 \cdot 1 = 4 - 4 = 0 $$

El discriminante es cero, por tanto la ecuación tiene una solución real doble.

Esto significa que la recta es tangente a la parábola.

Para encontrar el punto de tangencia, aplicamos la fórmula:

$$ x = \frac{-b \pm \sqrt{\Delta}}{2a} $$

$$ x = \frac{-(-2) \pm \sqrt{0}}{2 \cdot 1} $$

$$ x = \frac{2}{2} = 1 $$

Con \( x = 1 \), sustituimos en la ecuación de la recta para obtener la coordenada \( y \):

$$ y = 4x - 2 = 4 \cdot 1 - 2 = 2 $$

Por tanto, el punto de tangencia \( P \) tiene coordenadas \( (1, 2) \).

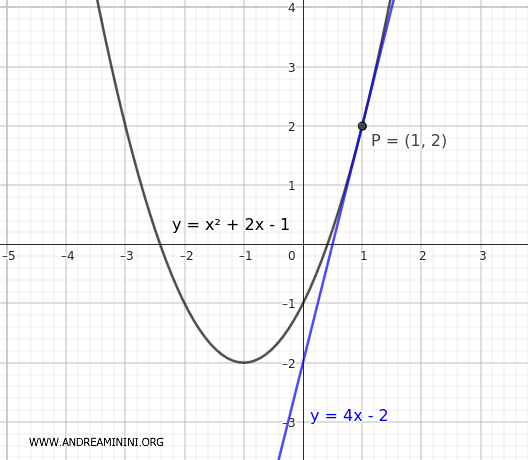
Demostración

La ecuación general de una parábola es:

$$ y = ax^2 + bx + c $$

y la de una recta no vertical:

$$ y = mx + q $$

Igualando ambas expresiones:

$$ ax^2 + bx + c = mx + q $$

$$ ax^2 + (b - m)x + (c - q) = 0 $$

Obtenemos así una ecuación cuadrática cuya resolución nos indica los puntos de intersección.

Las soluciones se determinan mediante la fórmula general:

$$ x = \frac{-b \pm \sqrt{b^2 - 4ac}}{2a} $$

Y según el valor del discriminante \( \Delta = b^2 - 4ac \), distinguimos tres situaciones:

• Si \( \Delta = 0 \), hay una única solución real: la recta es tangente a la parábola.
• Si \( \Delta > 0 \), hay dos soluciones reales distintas: la recta es secante.
• Si \( \Delta < 0 \), no hay soluciones reales: la recta es exterior.

Y así concluye el razonamiento.