Rectas tangentes a una parábola

Dada una parábola y un punto cualquiera \( P \) del plano, pueden existir dos, una o ninguna recta tangente a la parábola que pase por dicho punto.

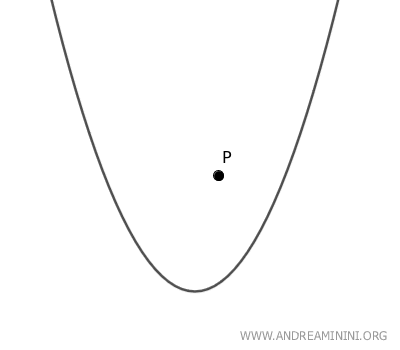
• Si el punto P se encuentra fuera de la parábola, existen dos rectas tangentes que pasan por él.
  
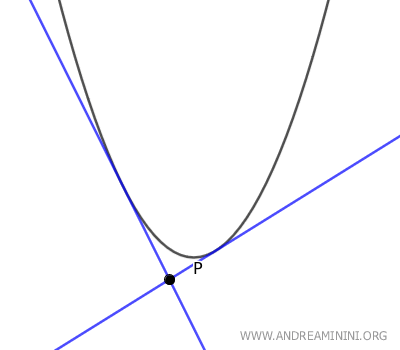
• Si el punto P pertenece a la parábola, existe una única recta tangente que pasa por él.
  
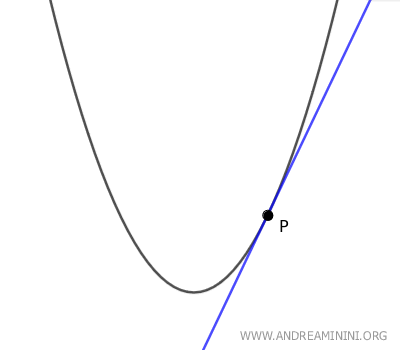
• Si el punto P está en el interior de la parábola, no existe ninguna recta tangente que lo atraviese.
  

Cómo determinar las rectas tangentes a una parábola

Para determinar cuántas rectas tangentes a una parábola pasan por un punto \( P \) y cuál es su naturaleza, partimos de la ecuación de la familia de rectas que pasan por el punto \( P(x_0, y_0) \):

$$ y - y_0 = m (x - x_0) $$

Queremos identificar cuáles de estas rectas intersectan la parábola dada por:

$$ y = ax^2 + bx + c $$

Así, planteamos un sistema de ecuaciones combinando la recta y la parábola:

$$ \begin{cases} y - y_0 = m (x - x_0) \\ y = ax^2 + bx + c \end{cases} $$

Las soluciones del sistema representan los puntos de intersección entre la parábola y las rectas de la familia, ya sean tangentes o secantes. 

Para aislar exclusivamente las tangentes, aplicamos la condición de tangencia.

Una recta es tangente a una curva si el sistema tiene una única solución, es decir, si la ecuación cuadrática resultante tiene una raíz doble, lo cual ocurre cuando el discriminante es cero:

$$ \Delta = b^2 - 4ac = 0 $$

Esta condición nos permite determinar el valor de la pendiente \( m \) para el cual la recta es tangente a la parábola.

Una vez calculado \( m \), lo sustituimos en la ecuación general de la recta para obtener la o las tangentes buscadas.

Un ejemplo práctico

Consideremos la parábola de ecuación:

$$ y = x^2 + 2x + 3 $$

Queremos encontrar las rectas tangentes a esta parábola que pasen por el punto \( P(-1,1) \).

La ecuación de la familia de rectas que pasan por \( P \) es:

$$ (y - y_0) = m(x - x_0) $$

Como las coordenadas de \( P(-1,1) \) son \( x_0 = -1 \) y \( y_0 = 1 \), tenemos:

$$ (y - 1) = m(x + 1) $$

Ahora buscamos qué rectas de esta familia intersectan la parábola:

$$ \begin{cases} y = x^2 + 2x + 3 \\ (y - 1) = m(x + 1) \end{cases} $$

$$ \begin{cases} y = x^2 + 2x + 3 \\ y = m(x + 1) + 1 \end{cases} $$

Igualando ambas expresiones de \( y \), obtenemos la ecuación:

$$ x^2 + 2x + 3 = m(x + 1) + 1 $$

$$ x^2 + 2x + 3 = mx + m + 1 $$

$$ x^2 + (2 - m)x + (3 - m - 1) $$

$$ x^2 + (2 - m)x + (2 - m) $$

El discriminante de esta ecuación cuadrática es:

$$ \Delta = b^2 - 4ac $$

Con coeficientes \( a = 1 \), \( b = (2 - m) \), \( c = (2 - m) \), tenemos:

$$ \Delta = (2 - m)^2 - 4(2 - m) $$

$$ \Delta = m^2 - 4 $$

Aplicamos la condición de tangencia:

$$ \Delta = m^2 - 4 = 0 $$

Resolvemos la ecuación:

$$ m^2 - 4 = 0 $$

Usamos la fórmula general:

$$ m = \frac{-b \pm \sqrt{b^2 - 4ac}}{2a} $$

Con \( a = 1 \), \( b = 0 \), \( c = -4 \), obtenemos:

$$ m = \frac{0 \pm \sqrt{16}}{2} $$

$$ m = \begin{cases} -2 \\ 2 \end{cases} $$

Hay dos soluciones distintas, por tanto existen dos rectas tangentes a la parábola que pasan por \( P(-1,1) \).

Reemplazamos cada valor de \( m \) en la ecuación de la recta:

• Si \( m = -2 \) $$ (y - 1) = -2(x + 1) $$ $$ y = -2x - 2 + 1 $$ $$ y = -2x - 1 $$
• Si \( m = 2 \) $$ (y - 1) = 2(x + 1) $$ $$ y = 2x + 2 + 1 $$ $$ y = 2x + 3 $$

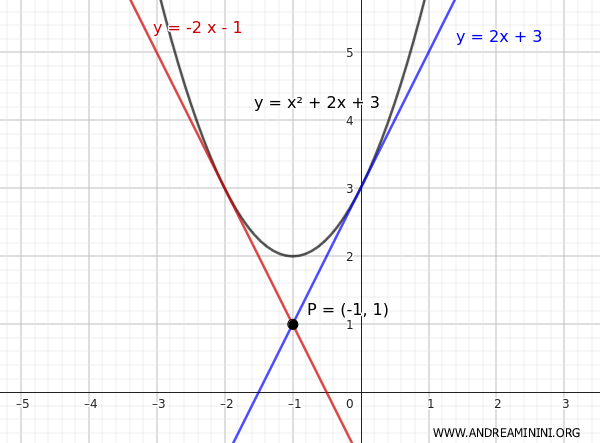
Las rectas tangentes a la parábola que pasan por el punto \( P(-1,1) \) son:

• $ y = -2x - 1 $
• $ y = 2x + 3 $

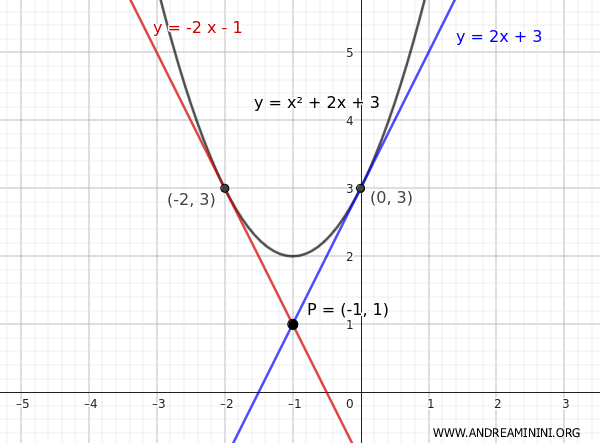
A continuación se muestra la representación gráfica de la solución:

Para hallar las coordenadas de los puntos de tangencia, resolvemos los sistemas formados por las ecuaciones de la parábola y de cada tangente. El primer sistema es:

$$ \begin{cases} y = x^2 + 2x + 3 \\ y = -2x - 1 \end{cases} $$

$$ \Rightarrow -2x - 1 = x^2 + 2x + 3 $$

$$ \Rightarrow x^2 + 4x + 4 = 0 $$

Como \( \Delta = 0 \), la solución es única: \( x = -2 \)

$$ y = -2(-2) - 1 = 3 $$

Por tanto, uno de los puntos de tangencia tiene coordenadas (-2, 3)

El segundo sistema es:

$$ \begin{cases} y = x^2 + 2x + 3 \\ y = 2x + 3 \end{cases} $$

$$ \Rightarrow 2x + 3 = x^2 + 2x + 3 $$

$$ \Rightarrow x^2 = 0 \Rightarrow x = 0 $$

$$ y = 2(0) + 3 = 3 $$

El otro punto de tangencia es (0, 3)

Y así sucesivamente.