Haz de parábolas
Un haz de parábolas (también llamado familia de parábolas) es una combinación lineal de dos parábolas base, conocidas como parábolas generadoras del haz.
Por ejemplo, dadas dos parábolas generadoras en forma implícita, siendo \( a_1 \ne 0 \):
$$ y + a_1 x^2 + b_1 x + c_1 = 0 $$
y \( a_2 \ne 0 \):
$$ y + a_2 x^2 + b_2 x + c_2 = 0 $$
el haz de parábolas se expresa como:
$$ (y + a_1 x^2 + b_1 x + c_1) + \lambda \cdot (y + a_2 x^2 + b_2 x + c_2) = 0 $$
donde \(\lambda \in \mathbb{R} \) es un parámetro real.
Al variar \(\lambda\), se obtienen todas las parábolas que pertenecen al haz.
Las parábolas de un haz pueden intersectarse en uno, dos o ningún punto del plano, denominados puntos base del haz.
Nota: Dicho de otro modo, un haz de parábolas es una familia de parábolas que depende de un parámetro variable, y su forma concreta está determinada por cómo varían los coeficientes de la ecuación cuadrática que las define. Cuando \(\lambda = 0\), se recupera la primera parábola: $$ (y + a_1 x^2 + b_1 x + c_1) + 0 \cdot (y + a_2 x^2 + b_2 x + c_2) = 0 $$ $$ y + a_1 x^2 + b_1 x + c_1 = 0 $$ Sin embargo, ningún valor real de \(\lambda\) permite obtener exactamente la segunda parábola. Por lo tanto, esta combinación lineal representa todas las combinaciones posibles salvo una (la segunda parábola). Para incluir también esa parábola, es necesario introducir dos parámetros reales: $$ \lambda_1 \cdot (y + a_1 x^2 + b_1 x + c_1) + \lambda_2 \cdot (y + a_2 x^2 + b_2 x + c_2) = 0 $$ donde \( \lambda_1, \lambda_2 \in \mathbb{R} \).
Otra forma equivalente y más general de representar el haz es:
$$ (a_1 + \lambda a_2 ) x^2 + (b_1 + \lambda b_2) x + (1 + \lambda) y + c_1 + \lambda c_2 = 0 $$
Esta forma es especialmente útil porque puede reescribirse como:
$$ A x^2 + B x + C y + D = 0 $$
donde, en este caso:
$$ A = a_1 + \lambda a_2 $$
$$ B = b_1 + \lambda b_2 $$
$$ C = 1 + \lambda $$
$$ D = c_1 + \lambda c_2 $$
Esta expresión permite calcular el vértice y el foco aplicando las fórmulas generales para una parábola.
- Foco
$$ F \begin{pmatrix} - \frac{B}{2A}, \frac{1 - \Delta}{4A} \end{pmatrix} $$ - Vértice
$$ V \begin{pmatrix} - \frac{B}{2A}, - \frac{\Delta}{4A} \end{pmatrix} $$ - Directriz
$$ y = - \frac{1 + \Delta}{4A} $$ - Eje de simetría
$$ x = - \frac{B}{2A} $$
Donde A, B y C son los coeficientes de la ecuación general del haz \( y = Ax^2 + Bx + C \), y el discriminante se define como \( \Delta = B^2 - 4AC \).
Nota: Para que se trate efectivamente de un haz de parábolas, el término cuadrático debe estar presente, como ocurre en cualquier parábola. Es decir, el coeficiente A no puede ser nulo (\( A \ne 0 \)).
Un ejemplo práctico
Consideremos dos parábolas generadoras:
$$ p_1: y = x^2 - 3x + 2 $$
$$ p_2: y = -x^2 + 5x - 4 $$
Las escribimos ahora en forma implícita:
$$ p_1: y - x^2 + 3x - 2 = 0 $$
$$ p_2: y + x^2 - 5x + 4 = 0 $$
En este caso, las dos parábolas se intersectan en los puntos A(1,0) y B(3,2).
Estos puntos son los puntos base del haz de parábolas.

El haz generado por la combinación lineal de ambas parábolas es:
$$ p_1 + \lambda \cdot p_2 = 0 $$
$$ (y - x^2 + 3x - 2) + \lambda \cdot (y + x^2 - 5x + 4) = 0 $$
$$ (\lambda - 1) x^2 + (3 - 5\lambda) x + (1 + \lambda) y - 2 + 4\lambda = 0 $$
Al variar el valor de \(\lambda\), obtenemos todas las parábolas del haz que pasan por los puntos de intersección de las generadoras.

Para obtener la ecuación del haz, también podríamos haber utilizado cualquier otro par de parábolas del mismo haz, incluidas las parábolas degeneradas, que en ciertos valores de \(\lambda\) se convierten en rectas.
Ejemplo: Para determinar la ecuación del haz de parábolas, también se pueden utilizar las parábolas degeneradas del haz. Supongamos que queremos obtener la ecuación del haz formado por dos parábolas que se cortan en los puntos A(1,0) y B(3,2). Cuando las generadoras se intersectan, dos parábolas degeneran en rectas. Una de ellas se transforma en una recta que une los dos puntos base A y B; la otra degenera en dos rectas paralelas al eje de simetría, cada una pasando por uno de los puntos base.
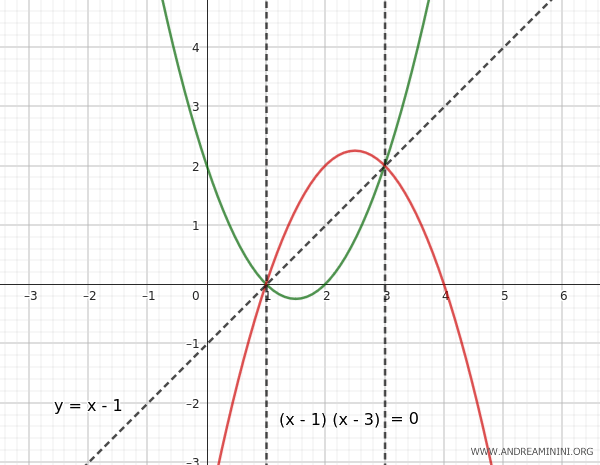
Para hallar el haz de parábolas, partimos de esas parábolas degeneradas. La ecuación de la recta que pasa por los puntos A(x1, y1) = (1,0) y B(x2, y2) = (3,2) es la siguiente:
$$ \frac{y - y_1}{y_2 - y_1} = \frac{x - x_1}{x_2 - x_1} $$
$$ \frac{y - 0}{2 - 0} = \frac{x - 1}{3 - 1} $$
$$ \frac{y}{2} = \frac{x - 1}{2} $$
$$ y = x - 1 $$
$$ y - x + 1 = 0 $$
La segunda parábola tiene raíces en 1 y 3, por lo tanto es el producto de los binomios \((x - 1)\) y \((x - 3)\).
$$ (x - 1)(x - 3) = 0 $$
Así, la ecuación del haz es la combinación lineal de estas dos parábolas degeneradas:
$$ y - x + 1 + \lambda [(x - 1)(x - 3)] = 0 $$
El resultado final es siempre el mismo.Tipos de parábolas generadoras
Un haz de parábolas puede estar definido por parábolas secantes, tangentes, externas o congruentes, con o sin puntos comunes. Para simplificar, nos limitaremos al caso de parábolas verticales, es decir, con eje paralelo al eje y.
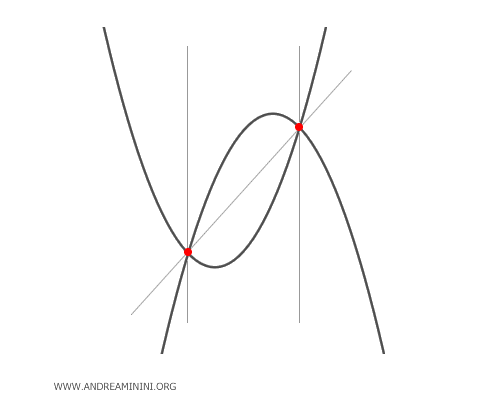
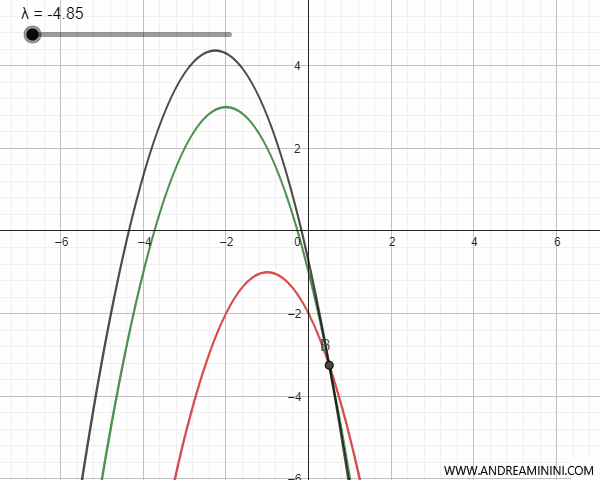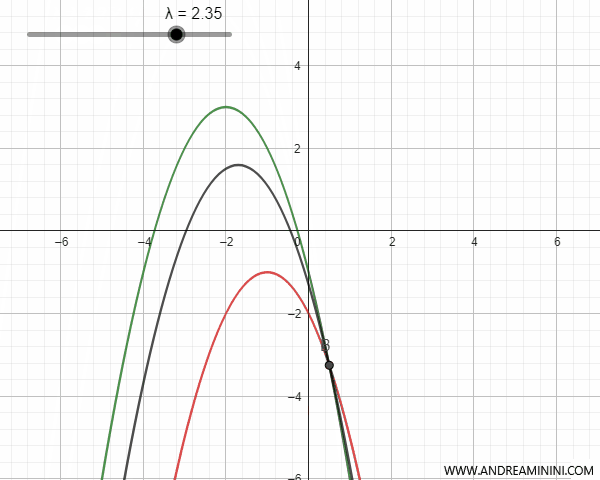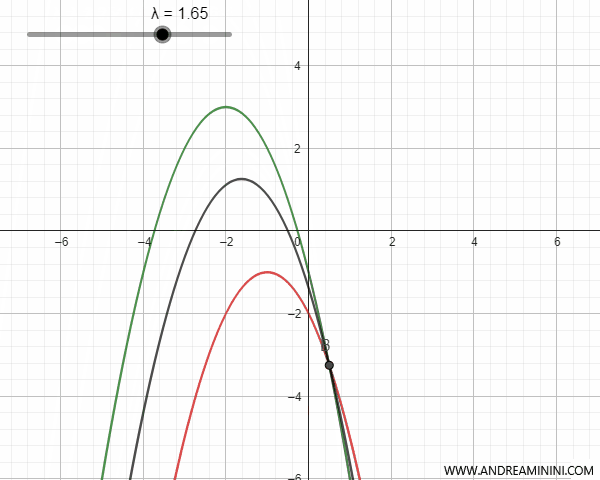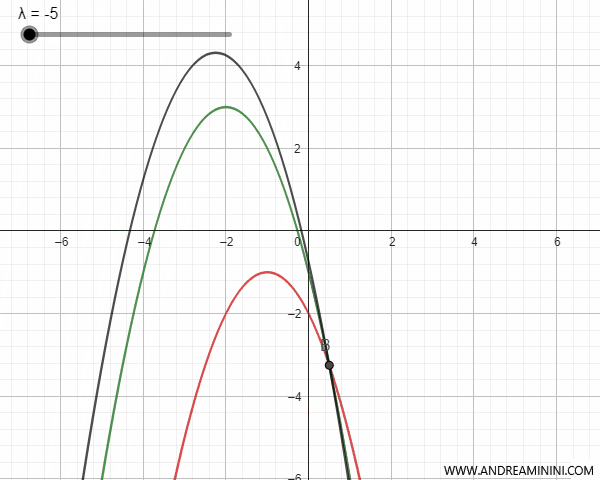
- Parábolas secantes
Las parábolas secantes se cruzan en dos puntos, que coinciden con los puntos base del haz. Para ciertos valores del parámetro \(\lambda\), la parábola correspondiente al haz degenera en una recta que pasa por los puntos base, y recibe el nombre de parábola degenerada.
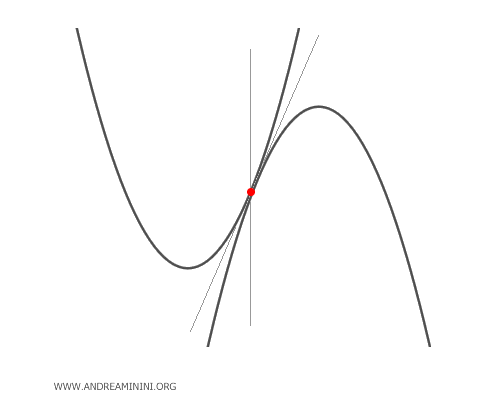
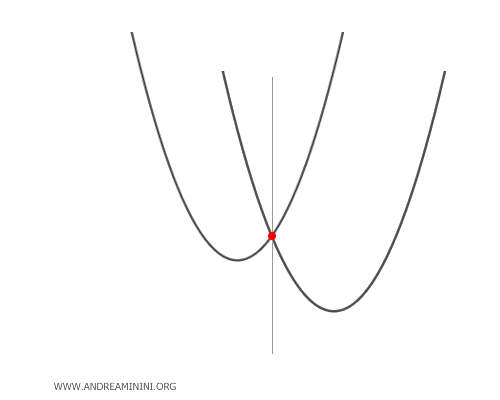
- Parábolas tangentes
Estas parábolas comparten un único punto de intersección, que corresponde al único punto base del haz. Para ciertos valores de \(\lambda\), la parábola generada degenera en una recta que pasa por dicho punto: en concreto, se trata de la recta tangente y de una recta paralela al eje de simetría.
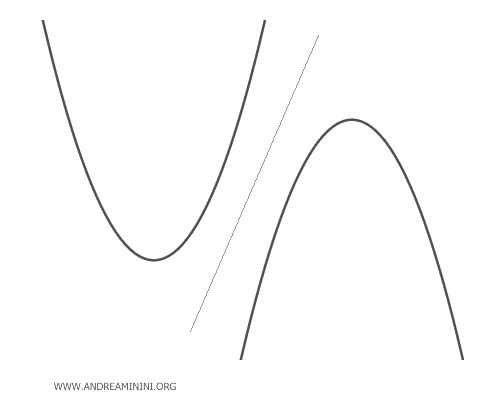
- Parábolas externas
Estas parábolas no tienen ningún punto en común, por lo que el haz carece de puntos base. Para un determinado valor del parámetro \(\lambda\), la parábola generada puede degenerar en una recta situada entre ambas parábolas.
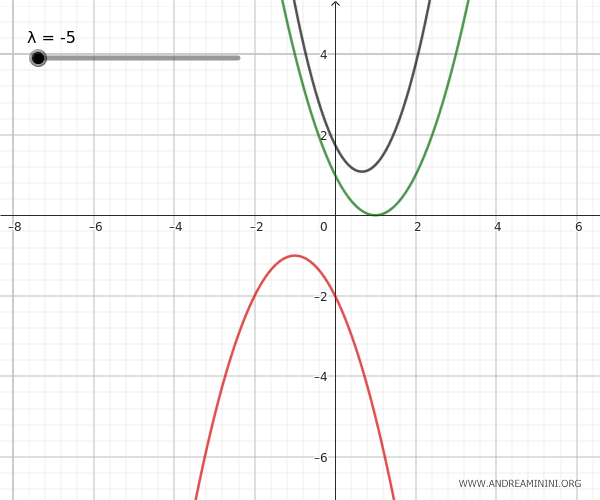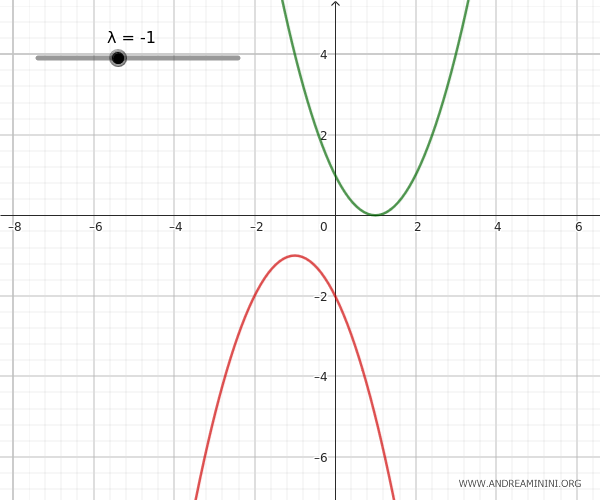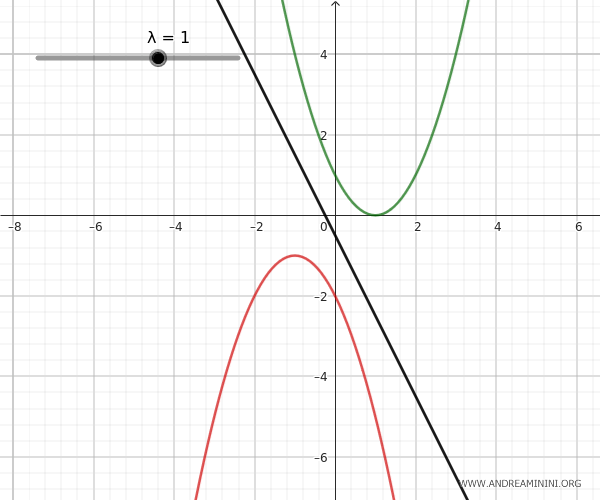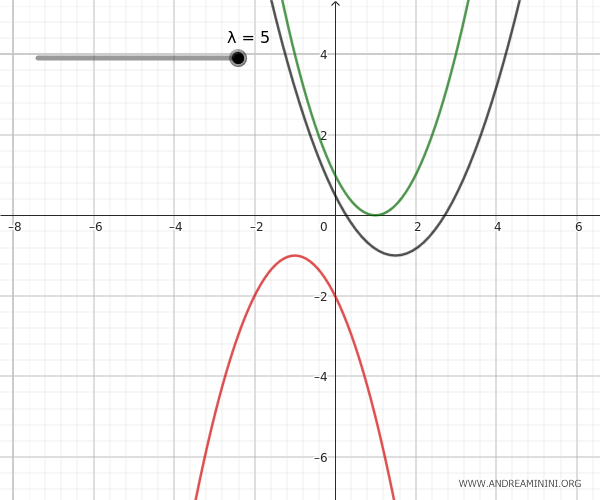
- Parábolas congruentes
Si dos parábolas congruentes comparten el mismo eje de simetría pero no se cortan, entonces no hay puntos base y el haz no degenera en ninguna recta.
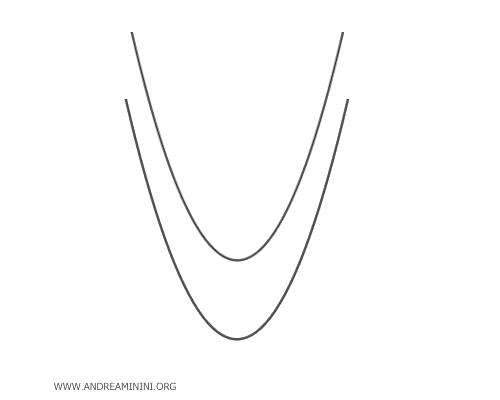
Por el contrario, si las parábolas congruentes tienen ejes paralelos pero distintos, se cortan en un punto base. En este caso, para ciertos valores de \(\lambda\), la parábola generada puede degenerar en una recta paralela al eje de simetría que pasa por dicho punto.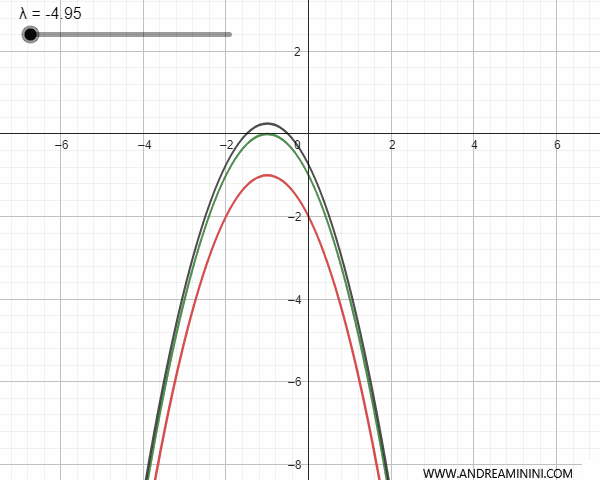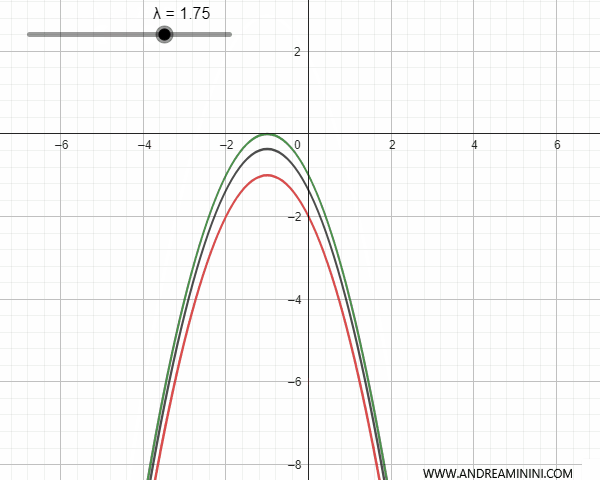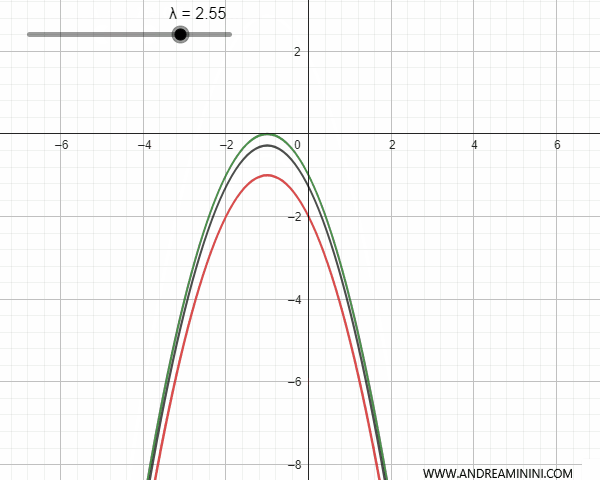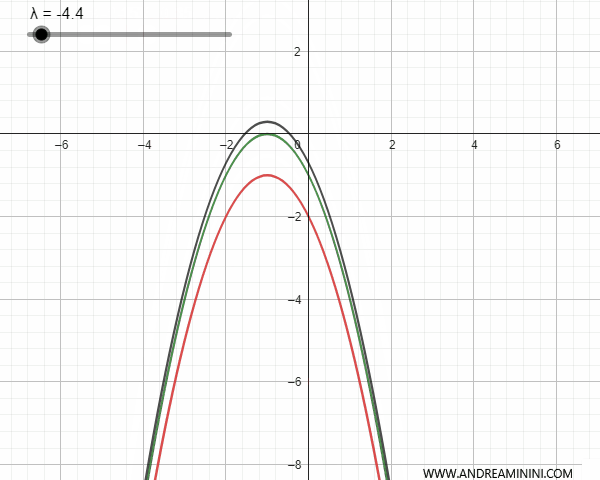
Cómo determinar las ecuaciones de las parábolas generadoras de un haz
Para hallar las ecuaciones de las parábolas generadoras de un haz, basta con reagrupar los términos en función del parámetro \(\lambda\).
La primera parábola generadora se obtiene evaluando la expresión con \(\lambda = 0\).
La segunda se obtiene anulando el término que multiplica a \(\lambda\).
Ejemplo
Consideremos la siguiente ecuación del haz:
$$ (\lambda - 1) x^2 + (3 - 5\lambda) x + (1 + \lambda) y - 2 + 4\lambda = 0 $$
Reagrupamos los términos en función de \(\lambda\):
$$ (\lambda - 1) x^2 - 5\lambda x + 3x + \lambda y + y + 4\lambda - 2 = 0 $$
$$ \lambda (x^2 - 5x + y + 4) - x^2 + 3x + y - 2 = 0 $$
La primera generadora se obtiene evaluando con \(\lambda = 0\):
$$ -x^2 + 3x + y - 2 = 0 $$
Es decir, \( y = x^2 - 3x + 2 \).
La segunda generadora se obtiene igualando a cero el coeficiente de \(\lambda\):
$$ x^2 - 5x + y + 4 = 0 \Rightarrow y = -x^2 + 5x - 4 $$
Hemos determinado así ambas parábolas generadoras del haz.
Cómo encontrar los puntos base de un haz de parábolas
Para identificar los puntos base de un haz de parábolas, es necesario resolver el sistema formado por sus generadoras.
- Si el sistema admite dos soluciones, existen dos puntos base y las parábolas se intersectan.
- Si solo hay una solución, hay un único punto base. En ese caso, las parábolas son tangentes o bien congruentes con ejes distintos; conviene entonces comprobar si se cumple la condición de tangencia.
- Si el sistema no tiene solución, no hay puntos base. Las parábolas pueden ser externas o congruentes con ejes coincidentes.
Ejemplo
Sean las generadoras:
$$ y = x^2 - 3x + 2 $$
$$ y = -x^2 + 5x - 4 $$
Igualando ambas expresiones de \( y \):
$$ x^2 - 3x + 2 = -x^2 + 5x - 4 $$
Llevamos todos los términos a un mismo lado:
$$ 2x^2 - 8x + 6 = 0 $$
Dividimos por 2 para simplificar:
$$ x^2 - 4x + 3 = 0 $$
Resolvemos mediante la fórmula cuadrática:
$$ x = \frac{-b \pm \sqrt{b^2 - 4ac}}{2a} $$
con \( a = 1 \), \( b = -4 \), \( c = 3 \):
$$ x = \frac{4 \pm \sqrt{16 - 12}}{2} = \frac{4 \pm 2}{2} $$
Entonces:
$$ x = 3 \quad \text{y} \quad x = 1 $$
Calculamos ahora los correspondientes valores de \( y \):
- Para \( x = 1 \): \( y = 1 - 3 + 2 = 0 \)
- Para \( x = 3 \): \( y = 9 - 9 + 2 = 2 \)
Por tanto, los puntos base del haz son \( (1, 0) \) y \( (3, 2) \).
Como hay dos puntos distintos, las parábolas son secantes.
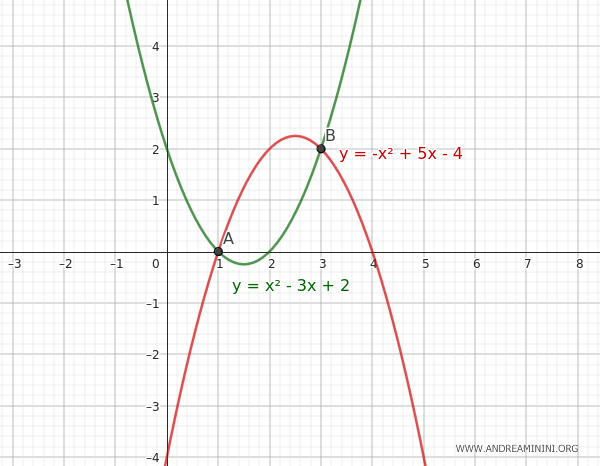
Y así sucesivamente.