Intersección entre una parábola y una recta

Una parábola puede intersectar una recta en, como máximo, dos puntos distintos.

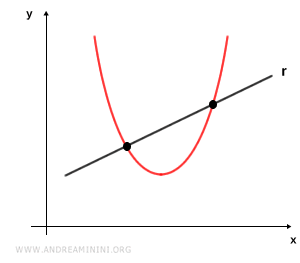
• Recta secante
  Se denomina secante a una recta que corta la parábola en dos puntos distintos.
  
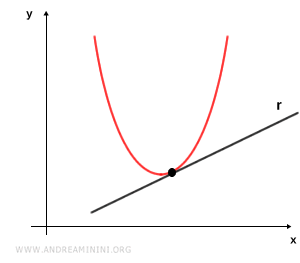
• Recta tangente
  Una recta es tangente si toca la parábola en un único punto y no es paralela a su eje de simetría.
  
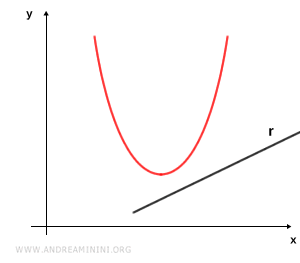
• Recta exterior
  Se dice que una recta es exterior cuando no intersecta la parábola en ningún punto.
  
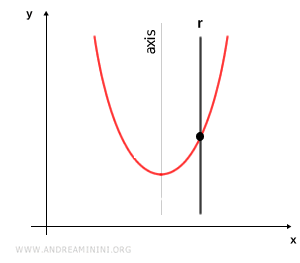
• Recta paralela al eje de la parábola
  Una recta es paralela al eje de la parábola si mantiene la misma dirección que dicho eje. Aunque en este caso puede haber un solo punto de intersección, la recta no se considera tangente.
  

Cómo determinar los puntos de intersección entre una parábola y una recta

Para encontrar los puntos de intersección entre una parábola y una recta no paralela a su eje, se plantea un sistema de ecuaciones en el que interviene una expresión cuadrática.

$$ \begin{cases} y = ax^2 + bx + c \\ \\ y = mx + q \end{cases} $$

La primera ecuación representa la parábola.

La segunda corresponde a la recta.

Como \( y = ax^2 + bx + c \) y \( y = mx + q \), igualamos ambas expresiones:

$$ ax^2 + bx + c = mx + q $$

De ahí se obtiene una ecuación cuadrática:

$$ ax^2 + bx - mx + c - q = 0 $$

$$ ax^2 + x(b - m) + (c - q) = 0 $$

Definimos \( a' = a \), \( b' = b - m \), y \( c' = c - q \), lo que nos lleva a:

$$ a'x^2 + b'x + c' = 0 $$

Ahora calculamos el discriminante de dicha ecuación:

$$ \Delta = b'^2 - 4a'c' $$

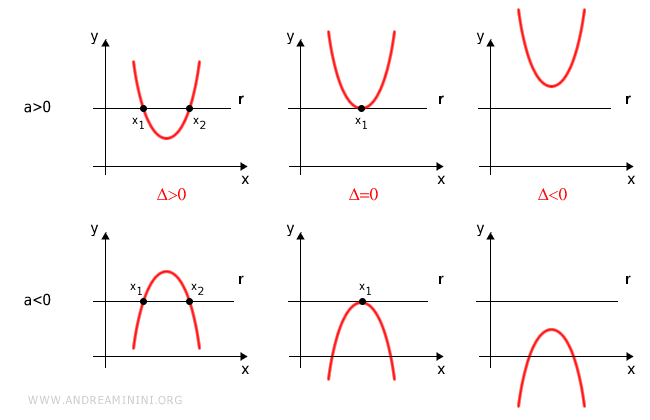
Según el valor de \( \Delta \), existen tres casos posibles:

• Δ > 0
  Si el discriminante es positivo, la recta es secante a la parábola. En este caso, la ecuación cuadrática tiene dos soluciones reales distintas que determinan los puntos de intersección.
• Δ = 0
  Si el discriminante es cero, la recta es tangente. La solución doble de la ecuación proporciona las coordenadas exactas del punto de tangencia.
• Δ < 0
  Si el discriminante es negativo, la recta es exterior a la parábola y no hay puntos de intersección.

Ejemplo práctico

Vamos a determinar si la recta

$$ y = -2x + 6 $$

es secante, tangente o exterior con respecto a la parábola

$$ y = -2x^2 + 2x + 4 $$

Igualamos ambas expresiones:

$$ -2x + 6 = -2x^2 + 2x + 4 $$

$$ 2x^2 - 2x - 2x + 6 - 4 = 0 $$

$$ 2x^2 - 4x + 2 = 0 $$

Calculamos el discriminante:

$$ \Delta = b^2 - 4ac = (-4)^2 - 4(2)(2) = 16 - 16 = 0 $$

Como \( \Delta = 0 \), la recta es tangente a la parábola.

Para hallar el punto de tangencia, resolvemos la ecuación cuadrática:

$$ x = \frac{-b \pm \sqrt{\Delta}}{2a} $$

$$ x = \frac{-(-4) \pm \sqrt{0}}{2(2)} $$

$$ x = \frac{4}{4} = 1 $$

Una vez obtenido \( x = 1 \), sustituimos en la ecuación de la recta para hallar el valor correspondiente de \( y \):

$$ y = -2x + 6 $$

$$ y = -2(1) + 6 = 4 $$

Por tanto, el punto de tangencia es \( (1, 4) \).

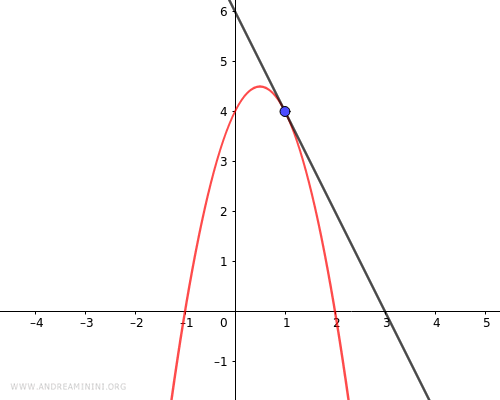
Así se determina la intersección entre una recta y una parábola.