Cómo determinar la ecuación de una parábola a partir del foco y el vértice
Para obtener la ecuación de una parábola cuyo eje es paralelo al eje y, conociendo las coordenadas del vértice \( V(h, k) \) y del foco \( F(h, k + p) \), basta seguir estos pasos:
- Determinar la distancia entre el vértice y el foco
La distancia \( p \) entre el vértice y el foco se obtiene restando la coordenada y del vértice de la del foco ($ k + p $ y $ k $, respectivamente): $$ p = (k + p) - k = p $$ - Escribir la ecuación de la parábola
La forma canónica de una parábola con vértice \((h, k)\) y eje de simetría paralelo al eje y es:
$$ (x - h)^2 = 4p(y - k) $$
Ejemplo práctico
Consideremos una parábola con vértice \((h, k) = (2, 3)\) y foco \((2, 5)\).
Queremos hallar su ecuación.
Primero calculamos la distancia entre el foco y el vértice:
$$ p = 5 - 3 = 2 $$
Luego sustituimos los valores en la ecuación general:
$$ (x - h)^2 = 4p(y - k) $$
Con \( p = 2 \), \( h = 2 \) y \( k = 3 \), se tiene:
$$ (x - 2)^2 = 8(y - 3) $$
Por lo tanto, la ecuación de la parábola con vértice \((2, 3)\) y foco \((2, 5)\) es:
$$ (x - 2)^2 = 8(y - 3) $$
Si desarrollamos la ecuación, obtenemos:
$$ x^2 - 4x + 4 = 8y - 24 $$
$$ 8y = x^2 - 4x + 28 $$
$$ y = \frac{x^2}{8} - \frac{x}{2} + \frac{7}{2} $$
La gráfica correspondiente es la siguiente:
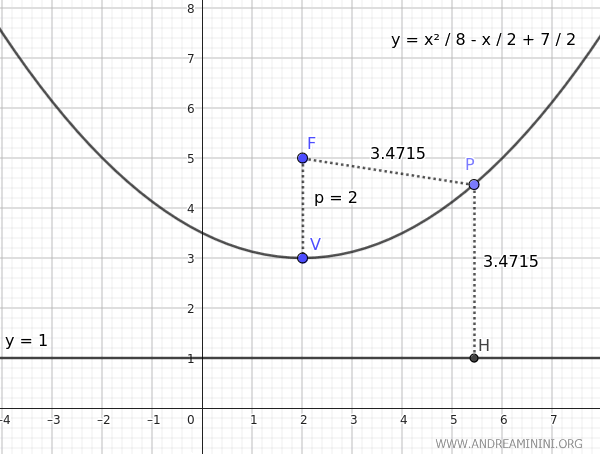
Nota: Dado que la directriz es perpendicular al eje de simetría de la parábola y está a la misma distancia del vértice que el foco, se deduce que su ecuación es y = 1. Esta relación permite comprobar que, para cualquier punto P sobre la parábola, la distancia al foco F es igual a la distancia a la directriz.
Este es el procedimiento para deducir la ecuación de una parábola conociendo las coordenadas del vértice y del foco.
Y así sucesivamente.