Fórmula de la recta tangente a una parábola

La fórmula de la recta tangente a una parábola permite determinar la ecuación de la tangente en un punto \( P(x_0, y_0) \) perteneciente a la curva. $$ \frac{y + y_0}{2} = ax_0 x + b \left( \frac{x + x_0}{2} \right) + c $$ Aquí, \( a \), \( b \) y \( c \) son los coeficientes de la parábola \( y = ax^2 + bx + c \).

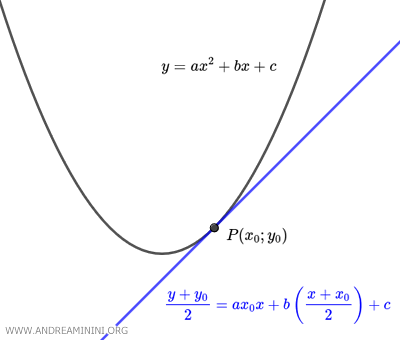
Esta expresión se deduce a partir de la ecuación general de la parábola:

$$ y = ax^2 + bx + c $$

Los términos cuadráticos y lineales se sustituyen de la siguiente manera:

$$ x^2 \rightarrow x_0x $$

$$ x \rightarrow \frac{x + x_0}{2} $$

$$ y \rightarrow \frac{y + y_0}{2} $$

Así, obtenemos la fórmula:

$$ \frac{y + y_0}{2} = ax_0 x + b \left( \frac{x + x_0}{2} \right) + c $$

Nota: Esta fórmula es válida únicamente para calcular la tangente en un punto perteneciente a la parábola. No puede aplicarse a puntos exteriores. En realidad, se trata de un caso particular de la fórmula general de la tangente para las secciones cónicas aplicada a la parábola.

Ejemplo práctico

Tomemos la parábola:

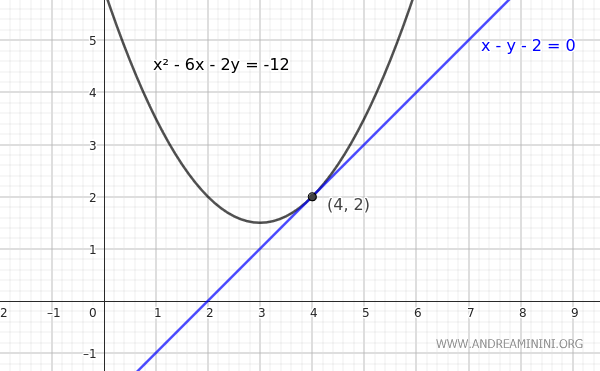
$$ x^2 - 6x - 2y = -12 $$

La reescribimos en su forma general:

$$ x^2 - 6x - 2y + 12 = 0 $$

Queremos hallar la ecuación de la tangente en el punto \( P(4, 2) \), que pertenece a la parábola.

Nota: Verificamos que el punto \( P(4, 2) \) pertenece a la curva sustituyendo \( x = 4 \) y \( y = 2 \): $$ 4^2 - 6 \cdot 4 - 2 \cdot 2 = -12 $$ $$ 16 - 24 - 4 = -12 $$ $$ -12 = -12 $$ La igualdad se cumple, por lo que el punto efectivamente pertenece a la parábola. Recordemos que la fórmula de la tangente solo es aplicable en este caso.

Sustituimos el término cuadrático \( x^2 \rightarrow x_0x \):

$$ x_0x - 6x - 2y + 12 = 0 $$

Ahora sustituimos el término lineal \( x \rightarrow \frac{x + x_0}{2} \):

$$ x_0x - 6 \cdot \frac{x + x_0}{2} - 2y + 12 = 0 $$

$$ x_0x - 3(x + x_0) - 2y + 12 = 0 $$

Luego sustituimos \( y \rightarrow \frac{y + y_0}{2} \):

$$ x_0x - 3(x + x_0) - 2 \cdot \frac{y + y_0}{2} + 12 = 0 $$

$$ x_0x - 3(x + x_0) - y - y_0 + 12 = 0 $$

Como \( x_0 = 4 \) y \( y_0 = 2 \), sustituimos:

$$ 4x - 3(x + 4) - y - 2 + 12 = 0 $$

$$ 4x - 3x - 12 - y + 10 = 0 $$

$$ x - y - 2 = 0 $$

Esta es la ecuación de la recta tangente a la parábola en el punto \( P(4, 2) \).

Demostración

Para demostrar esta fórmula, partimos de la ecuación general:

$$ y = ax^2 + bx + c $$

Consideramos un punto genérico \( P(x_0, y_0) \).

La familia de rectas que pasan por P tiene la forma:

$$ y - y_0 = m(x - x_0) $$

Para hallar las rectas que intersectan la parábola en P (ya sean secantes o tangentes), resolvemos el sistema:

$$ \begin{cases} y = ax^2 + bx + c \\ \\ y = m(x - x_0) + y_0 \end{cases} $$

Igualando ambas expresiones:

$$ ax^2 + bx + c = m(x - x_0) + y_0 $$

$$ ax^2 + bx + c - m(x - x_0) - y_0 = 0 $$

$$ ax^2 + x(b - m) + (mx_0 - y_0 + c) = 0 $$

En una ecuación cuadrática \( Ax^2 + Bx + C = 0 \), la suma de las raíces \( x_1 + x_2 \) viene dada por: $$ x_1 + x_2 = - \frac{B}{A} $$ Donde \( A = a \) y \( B = b - m \): $$ x_1 + x_2 = - \frac{b - m}{a} $$

En el caso de una tangente, ambas raíces coinciden: $$ x_1 = x_2 = x_0 $$ Por lo tanto: $$ 2x_0 = - \frac{b - m}{a} $$ De donde despejamos la pendiente \( m \): $$ m = 2a x_0 + b $$

Sustituyendo en la ecuación de la recta:

$$ y - y_0 = (2a x_0 + b)(x - x_0) $$

Desarrollamos:

$$ y - y_0 = 2a x_0 x - 2a x_0^2 + bx - b x_0 $$

Sabemos que \( y_0 = a x_0^2 + b x_0 + c \), por lo que:

$$ 2 y_0 = 2a x_0^2 + 2b x_0 + 2c $$

Sumando ambas expresiones:

\[ \begin{array}{rcl} y - y_0 & = & 2a x_0 x - 2a x_0^2 + b x - b x_0 \\ 2 y_0 & = & 2a x_0^2 + 2b x_0 + 2c \\ \hline y + y_0 & = & 2a x_0 x + b x + b x_0 + 2c \end{array} \]

Finalmente, dividiendo ambos lados entre 2:

$$ \frac{y + y_0}{2} = ax_0 x + b \left( \frac{x + x_0}{2} \right) + c $$

Así queda demostrada la fórmula de la recta tangente.

Y así sucesivamente.