Ecuación de una parábola que pasa por dos puntos y es tangente a una recta
Para determinar la ecuación de una parábola que pasa por dos puntos dados \((x_1, y_1)\) y \((x_2, y_2)\), y que además es tangente a una recta \(r\), se deben seguir los siguientes pasos:
- Plantear la ecuación general de la parábola: $$ y = ax^2 + bx + c $$
- Sustituir las coordenadas de los puntos conocidos \((x_1, y_1)\) y \((x_2, y_2)\) para obtener dos ecuaciones
- Añadir al sistema la condición de tangencia entre la parábola y la recta \(r\)
- Resolver el sistema para encontrar los coeficientes \(a\), \(b\) y \(c\) de la parábola
Ejemplo práctico
Una parábola pasa por los puntos A(2, 0) y B(0, 1), y es tangente a la recta \(4x + 8y - 7 = 0\).
Queremos determinar su ecuación.
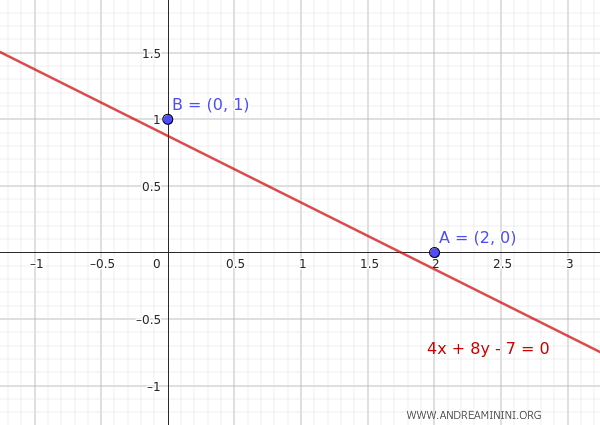
Sin embargo, los datos iniciales no indican si la parábola tiene eje vertical u horizontal.
Por tanto, es necesario analizar ambas posibilidades.
1] Parábola con eje paralelo al eje y
La ecuación general de una parábola con eje paralelo al eje \(y\) es:
$$ y = ax^2 + bx + c $$
Como primer paso, sustituimos las coordenadas de los puntos A(2, 0) y B(0, 1) en dicha ecuación para obtener dos relaciones:
Para el punto A(2, 0):
$$ y_1 = ax_1^2 + bx_1 + c $$
$$ 0 = a(2)^2 + b(2) + c $$
$$ 4a + 2b + c = 0 $$
Para el punto B(0, 1):
$$ y_2 = ax_2^2 + bx_2 + c $$
$$ 1 = a(0)^2 + b(0) + c $$
$$ c = 1 $$
Obtenemos entonces el sistema:
$$ \begin{cases} 4a + 2b + c = 0 \\ \\ c = 1 \end{cases} $$
A continuación, incorporamos la condición de tangencia con la recta \(4x + 8y - 7 = 0\).
Reescribimos la ecuación de la recta en forma explícita:
$$ y = -\frac{4x}{8} + \frac{7}{8} $$
$$ y = -\frac{x}{2} + \frac{7}{8} $$
Igualamos esta expresión con la de la parábola para hallar los puntos de intersección:
$$ ax^2 + bx + c = -\frac{x}{2} + \frac{7}{8} $$
$$ ax^2 + \left(b + \frac{1}{2}\right)x + c - \frac{7}{8} = 0 $$
Esta es una ecuación cuadrática cuyos ceros representan los puntos comunes entre la parábola y la recta.
Para que exista tangencia, dicha ecuación debe tener una única solución real, es decir, su discriminante debe anularse: \( \Delta = 0 \).
$$ \Delta = \left(b + \frac{1}{2} \right)^2 - 4a\left(c - \frac{7}{8} \right) = 0 $$
$$ \Delta = b^2 + b + \frac{1}{4} - 4ac + \frac{7a}{2} = 0 $$
Agregamos esta condición al sistema:
$$ \begin{cases} 4a + 2b + 1 = 0 \\ \\ c = 1 \\ \\ b^2 + b + \frac{1}{4} - 4a + \frac{7a}{2} = 0 \end{cases} $$
Simplificamos:
$$ \begin{cases} a = \frac{-2b - 1}{4} \\ \\ c = 1 \\ \\ b^2 + b + \frac{1}{4} - \frac{1}{2}a = 0 \end{cases} $$
Sustituimos \(a\) en la tercera ecuación:
$$ b^2 + b + \frac{1}{4} + \frac{2b + 1}{8} = 0 $$
$$ b^2 + b + \frac{b}{4} + \frac{3}{8} = 0 $$
$$ b^2 + \frac{5b}{4} + \frac{3}{8} = 0 $$
Resolvemos esta ecuación cuadrática. El discriminante es:
$$ \Delta = \left(\frac{5}{4}\right)^2 - 4 \cdot 1 \cdot \frac{3}{8} = \frac{25}{16} - \frac{12}{8} = \frac{1}{16} $$
Las soluciones son:
$$ b = \frac{-\frac{5}{4} \pm \sqrt{\frac{1}{16}}}{2} = \begin{cases} -\frac{1}{2} \\ \\ -\frac{3}{4} \end{cases} $$
El sistema entonces queda:
$$ \begin{cases} a = \frac{-2b - 1}{4} \\ \\ c = 1 \\ \\ b = \begin{cases} -\frac{1}{2} \\ \\ -\frac{3}{4} \end{cases} \end{cases} $$
Analizamos ambos casos:
- Si \( b = -\frac{1}{2} \), entonces \( a = \frac{1 - 1}{4} = 0 \). Como \( a = 0 \), esta solución se descarta ya que no corresponde a una parábola.
- Si \( b = -\frac{3}{4} \), entonces \( a = \frac{ \frac{3}{2} - 1 }{4} = \frac{1}{8} \). En este caso, los coeficientes son: \( a = \frac{1}{8} \), \( b = -\frac{3}{4} \), \( c = 1 \). Por tanto, la ecuación de la parábola es: $$ y = ax^2 + bx + c $$ $$ y = \frac{1}{8}x^2 - \frac{3}{4}x + 1 $$ La gráfica muestra claramente que la parábola pasa por los puntos A(2, 0) y B(0, 1), y es tangente a la recta \(4x + 8y - 7 = 0\).
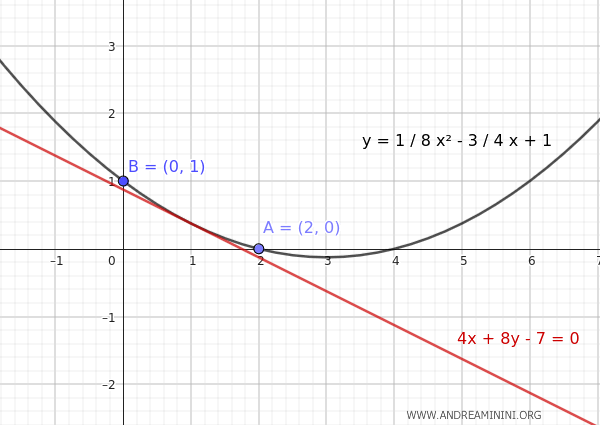
Nota. Otra forma de plantear la condición de tangencia consiste en escribir la ecuación de la recta en forma explícita: $$ y = -\frac{x}{2} + \frac{7}{8} $$ Así, se observa que la pendiente de la recta es \( -\frac{1}{2} \). Dado que en un punto de tangencia la pendiente de la curva coincide con la de la recta, se puede derivar la parábola para obtener su pendiente y luego igualarla a la de la recta. La derivada de la parábola \( y = ax^2 + bx + c \) es: $$ y' = 2ax + b $$ Por lo tanto, la condición de tangencia se expresa como: $$ 2ax + b = -\frac{1}{2} $$ $$ b = -\frac{1}{2} - 2ax $$ En este caso, el sistema a resolver queda así: $$ \begin{cases} 4a + 2b + c = 0 \\ \\ c = 1 \\ \\ b = -\frac{1}{2} - 2ax \end{cases} $$ La solución final será la misma, aunque con esta estrategia la incógnita \(x\) también interviene en los cálculos, lo que puede alargarlos o complicarlos.
2] Parábola con eje paralelo al eje x
La ecuación general de una parábola con eje paralelo al eje \(x\) es:
$$ x = ay^2 + by + c $$
Sustituimos las coordenadas de los puntos A(2, 0) y B(0, 1) en la ecuación:
Para el punto A(2, 0), con \( x_1 = 2 \) y \( y_1 = 0 \):
$$ x_1 = ay_1^2 + by_1 + c $$
$$ 2 = a(0)^2 + b(0) + c $$
$$ c = 2 $$
Para el punto B(0, 1), con \( x_2 = 0 \) y \( y_2 = 1 \):
$$ x_2 = ay_2^2 + by_2 + c $$
$$ 0 = a(1)^2 + b(1) + c $$
$$ a + b + c = 0 $$
Obtenemos así el siguiente sistema de ecuaciones:
$$ \begin{cases} c = 2 \\ \\ a + b + c = 0 \end{cases} $$
Incorporamos ahora la condición de tangencia con la recta \( 4x + 8y - 7 = 0 \).
Reescribimos la ecuación de la recta despejando \(x\):
$$ x = \frac{7 - 8y}{4} $$
$$ x = \frac{7}{4} - 2y $$
Igualamos esta expresión a la de la parábola para encontrar los puntos de intersección:
$$ ay^2 + by + c = \frac{7}{4} - 2y $$
$$ ay^2 + (b + 2)y + c - \frac{7}{4} = 0 $$
Como buscamos una tangencia, exigimos que el discriminante de esta ecuación cuadrática sea cero:
$$ \Delta = (b + 2)^2 - 4a \left(c - \frac{7}{4} \right) = 0 $$
Incorporamos esta condición al sistema anterior:
$$ \begin{cases} c = 2 \\ \\ a + b + c = 0 \\ \\ (b + 2)^2 - 4a \left(2 - \frac{7}{4} \right) = 0 \end{cases} $$
Simplificamos paso a paso:
$$ \begin{cases} c = 2 \\ \\ a + b + 2 = 0 \\ \\ b^2 + 4b + 4 - 4a \cdot \frac{1}{4} = 0 \end{cases} $$
$$ \begin{cases} c = 2 \\ \\ a = -2 - b \\ \\ b^2 + 4b + 4 - a = 0 \end{cases} $$
Sustituimos \(a\) en la tercera ecuación:
$$ b^2 + 4b + 4 + 2 + b = 0 $$
$$ b^2 + 5b + 6 = 0 $$
Calculamos el discriminante:
$$ \Delta = 5^2 - 4 \cdot 1 \cdot 6 = 25 - 24 = 1 $$
Las soluciones son:
$$ b = \frac{-5 \pm \sqrt{1}}{2} = \begin{cases} -3 \\ \\ -2 \end{cases} $$
Por tanto, obtenemos dos soluciones posibles:
- Si \( b = -3 \), entonces \( a = -2 - (-3) = 1 \). Los coeficientes de la parábola son \( a = 1 \), \( b = -3 \), \( c = 2 \), y su ecuación es: $$ x = ay^2 + by + c $$ $$ x = y^2 - 3y + 2 $$
- Si \( b = -2 \), entonces \( a = -2 - (-2) = 0 \), lo cual invalida la parábola ya que no habría término cuadrático. Esta solución debe descartarse.
La siguiente imagen muestra la gráfica de la parábola:
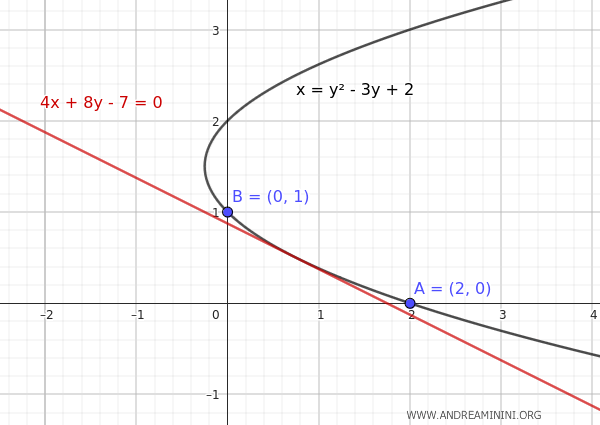
En este caso, se trata de una parábola con eje horizontal que pasa por los puntos A(2, 0) y B(0, 1), y es tangente a la recta \( 4x + 8y - 7 = 0 \).
Y así sucesivamente.