Ecuación en forma estándar de una parábola con eje paralelo al eje y

La ecuación en forma estándar de una parábola con vértice en \((h, k)\) y eje de simetría paralelo al eje \(y\) es $$ (x - h)^2 = 4p(y - k) $$. En esta expresión, \( p \) representa la distancia entre el foco \((x_F, y_F)\) y el vértice \((h, k)\): $$ p =  y_F - k $$

Esta ecuación se deriva de la definición geométrica de la parábola como el conjunto de puntos equidistantes de un punto fijo (el foco) y de una recta fija (la directriz).

El valor de \( p \) determina la dirección en la que se abre la parábola:

• Si \( p > 0 \), la parábola se abre hacia arriba.
• Si \( p < 0 \), se abre hacia abajo.

Esta forma resulta especialmente útil porque permite identificar con claridad la posición del vértice y la distancia entre el vértice y el foco, lo cual facilita el análisis de la parábola.

Un ejemplo práctico

El foco de una parábola se encuentra en las coordenadas \( F(3,2) \), y su vértice en \( V(3,1) \).

Se trata de una parábola cuyo eje de simetría es paralelo al eje \(y\), ya que foco y vértice comparten la misma coordenada \(x\): \( x = 3 \).

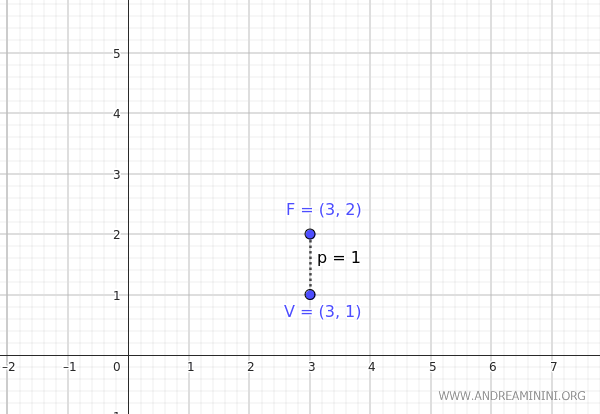
Para determinar la ecuación de la parábola, utilizamos la forma estándar:

$$ (x - h)^2 = 4p(y - k) $$

En este caso, la distancia entre el vértice y el foco es \( p = 2 - 1 = 1 \)

$$ (x - h)^2 = 4 \cdot 1 (y - k) $$

$$ (x - h)^2 = 4(y - k) $$

Como el vértice tiene coordenadas \( h = 3 \) y \( k = 1 \), sustituimos en la fórmula:

$$ (x - 3)^2 = 4(y - 1) $$

$$ x^2 - 6x + 9 = 4y - 4 $$

Por tanto, la ecuación de la parábola es

$$ y = \frac{x^2}{4} - \frac{3x}{2} + \frac{13}{4} $$

De este modo, hemos deducido la ecuación de la parábola a partir de su foco y vértice.

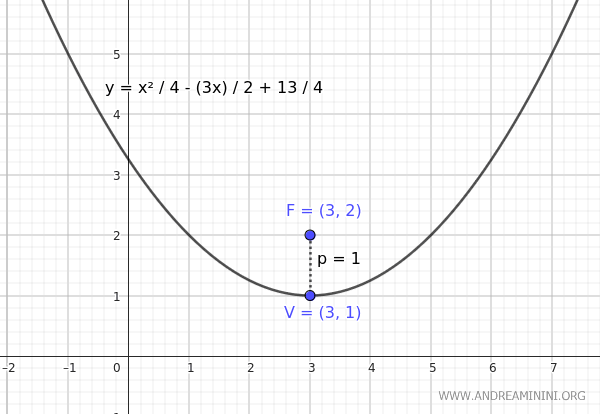
Verificación

En una parábola, la distancia entre el foco \( F \) y cualquier punto \( P \) de la curva siempre es igual a la distancia entre ese mismo punto \( P \) y la directriz.

Una vez que conocemos la ecuación cuadrática de la parábola, podemos determinar la ecuación de la directriz:

$$ y = - \frac{1 + \Delta}{4a} $$

Donde \( \Delta = b^2 - 4ac \) es el discriminante de la ecuación \( y = \frac{x^2}{4} - \frac{3x}{2} + \frac{13}{4} \)

Los coeficientes son \( a = \frac{1}{4} \), \( b = -\frac{3}{2} \), y \( c = \frac{13}{4} \)

$$ \Delta = b^2 - 4ac $$

$$ \Delta = \left(-\frac{3}{2}\right)^2 - 4 \cdot \frac{1}{4} \cdot \frac{13}{4} $$

$$ \Delta = \frac{9}{4} - \frac{13}{4} $$

$$ \Delta = \frac{-4}{4} = -1 $$

Entonces, la ecuación de la directriz es:

$$ y = - \frac{1 + \Delta}{4a} = - \frac{1 - 1}{4 \cdot \frac{1}{4}} = 0 $$

En este caso, la directriz coincide con el eje \(x\).

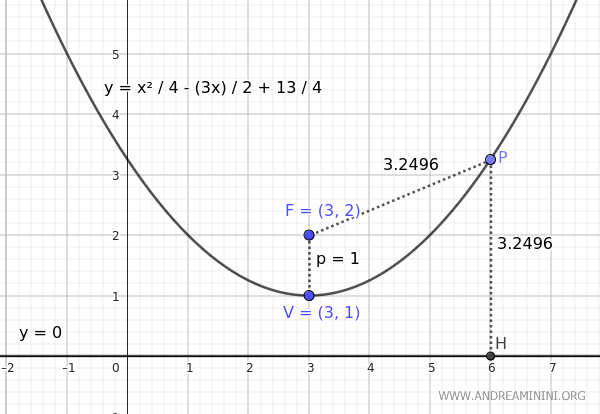
Para cualquier punto \( P \) en la parábola, la distancia al foco es igual a la distancia a la directriz (PF ≈ PH).

Por tanto, la ecuación obtenida es correcta.

Nota: En este ejemplo, he desarrollado todos los cálculos necesarios para hallar la directriz. Lo hice por exhaustividad, pero no es estrictamente necesario. También se puede llegar al mismo resultado de forma más directa: basta con recordar que la directriz es perpendicular (90°) al eje de simetría de la parábola (que en este caso es vertical) y se encuentra a la misma distancia del vértice que el foco, pero en sentido opuesto. Como el vértice está en (3,1) y la distancia al foco es 1, la directriz pasa por el punto (3,0), es decir, su ecuación es \( y = 0 \).

Demostración

Una parábola se define como el conjunto de puntos cuya distancia a un punto fijo, llamado foco \((h, k + p)\), es igual a su distancia a una recta fija, llamada directriz \( y = k - p \).

La distancia desde un punto de la parábola \( P(x, y) \) al foco \((h, k + p)\) es:

$$ \sqrt{(x - h)^2 + (y - (k + p))^2} $$

Y la distancia desde ese mismo punto \( P(x, y) \) a la directriz \( y = k - p \) es:

$$ |y - (k - p)| $$

Por definición, estas dos distancias son iguales:

$$ \sqrt{(x - h)^2 + (y - (k + p))^2} = |y - (k - p)| $$

Como la distancia es siempre positiva, podemos eliminar el valor absoluto y escribir:

$$ \sqrt{(x - h)^2 + (y - (k + p))^2} = y - (k - p) $$

Elevando al cuadrado ambos lados:

$$ (x - h)^2 + (y - (k + p))^2 = (y - (k - p))^2 $$

$$ (x - h)^2 + (y - k - p)^2 = (y - k + p)^2 $$

Desarrollando ambos lados:

$$ (x - h)^2 + (y - k)^2 - 2p(y - k) + p^2 = (y - k)^2 + 2p(y - k) + p^2 $$

Al cancelar los términos comunes:

$$ (x - h)^2 = 4p(y - k) $$

Por tanto, la ecuación en forma estándar de una parábola con vértice \((h, k)\) y eje de simetría paralelo al eje \(y\) es:

$$ (x - h)^2 = 4p(y - k) $$

Aquí, \( p \) representa la distancia entre el vértice y el foco, y el valor \( 4p \) determina cuán abierta o cerrada es la parábola.

A mayor \( p \), más ancha será la parábola; a menor \( p \), más estrecha.

En conclusión, la forma estándar \((x - h)^2 = 4p(y - k)\) se deduce directamente de la definición geométrica de parábola y de la relación entre el foco y la directriz.

Y así sucesivamente.