Ecuación de una parábola rotada con eje oblicuo

Para describir una parábola cuyo vértice está en \( (h, k) \) y cuyo eje de simetría forma un ángulo \(\alpha\) con el eje horizontal, debemos considerar que se trata de una parábola obtenida mediante una rotación isométrica del sistema de coordenadas.

Por ejemplo, si rotamos un punto \( (x, y) \) un ángulo \(-\alpha\), sus nuevas coordenadas \( (x', y') \) se obtienen mediante la siguiente transformación:

$$ x' = (x - h) \cos(\alpha) + (y - k) \sin(\alpha) $$

$$ y' = -(x - h) \sin(\alpha) + (y - k) \cos(\alpha) $$

Si la ecuación original de la parábola (con eje paralelo al eje y) es:

$$ y = ax^2 $$

entonces, en el nuevo sistema de referencia \( (x', y') \), la parábola adopta la forma estándar:

$$ y' = a (x')^2 $$

Al sustituir las expresiones de \( x' \) y \( y' \) en esta ecuación, obtenemos la forma rotada de la parábola:

$$ -(x - h) \sin(\alpha) + (y - k) \cos(\alpha) = a \left[ (x - h) \cos(\alpha) + (y - k) \sin(\alpha) \right]^2 $$

Alternativamente, si la parábola se expresa en su forma canónica con eje vertical, \( (x - h)^2 = 4p(y - k) \), tras una rotación de ángulo \(\alpha\), la ecuación se transforma en:

$$ \left[(x - h) \cos(\alpha) + (y - k) \sin(\alpha)\right]^2 = 4p \left[-(x - h) \sin(\alpha) + (y - k) \cos(\alpha)\right] $$

Estas son las expresiones generales que describen una parábola con eje de simetría oblicuo.

Ejemplo práctico

Consideremos una parábola con vértice en \( V(h, k) = (3, 5) \) y eje inclinado 45°, es decir, \( \alpha = 45^\circ \) o \( \alpha = \frac{\pi}{4} \):

Partimos de la ecuación rotada:

$$ \left[(x - h) \cos(\alpha) + (y - k) \sin(\alpha)\right]^2 = 4p \left[-(x - h) \sin(\alpha) + (y - k) \cos(\alpha)\right] $$

Sustituimos \( h = 3 \), \( k = 5 \) y \( \alpha = 45^\circ \):

$$ \left[(x - 3) \cos(45^\circ) + (y - 5) \sin(45^\circ)\right]^2 = 4p \left[-(x - 3) \sin(45^\circ) + (y - 5) \cos(45^\circ)\right] $$

Como \( \cos(45^\circ) = \sin(45^\circ) = \frac{1}{\sqrt{2}} \), obtenemos:

$$ \left[(x - 3) \cdot \frac{1}{\sqrt{2}} + (y - 5) \cdot \frac{1}{\sqrt{2}}\right]^2 = 4p \left[-(x - 3) \cdot \frac{1}{\sqrt{2}} + (y - 5) \cdot \frac{1}{\sqrt{2}}\right] $$

Factorizando y simplificando:

$$ \left[(x - 3) + (y - 5)\right]^2 = 8p \left[(y - 5) - (x - 3)\right] $$

Desarrollando ambos miembros se obtiene la ecuación explícita de la parábola rotada.

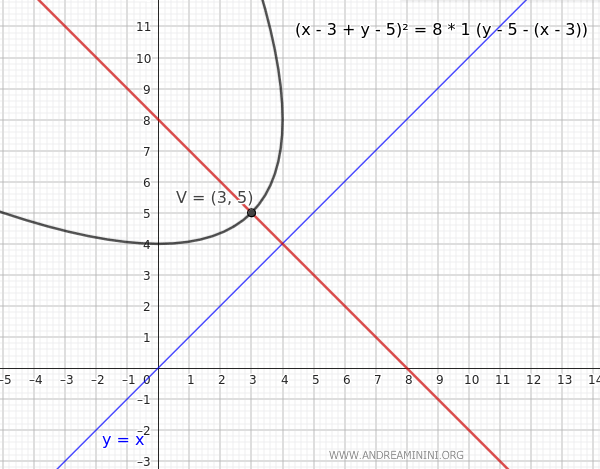
Y así sucesivamente.