Función Directamente Proporcional

Una función directamente proporcional se expresa como $$ y = k \cdot x $$, donde k es una constante real distinta de cero (k≠0).

En este caso, se dice que las variables x e y son directamente proporcionales.

Este tipo de funciones presentan las siguientes propiedades:

• La razón entre las variables, k=y/x, permanece constante para cualquier valor de x (excepto cuando x=0). $$ k = \frac{y}{x} $$
• Si una de las variables es cero (x=0), la otra también lo será (y=0).

Nota. De ello se deduce que toda función directamente proporcional pasa necesariamente por el origen (0,0). Cuando x es cero, y también debe serlo. En consecuencia, la gráfica de una función directamente proporcional siempre atraviesa el origen O. Veamos un ejemplo sencillo:

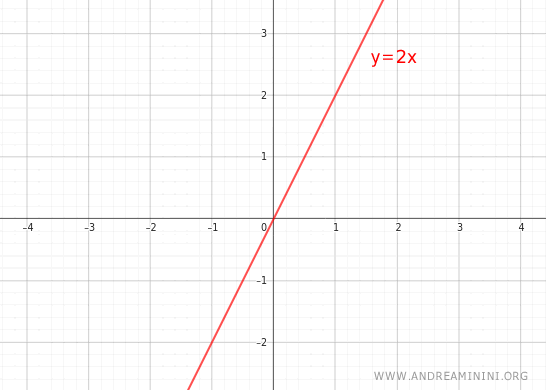
Un Ejemplo Práctico

Consideremos la función:

$$ y = 2x $$

Podemos elaborar la siguiente tabla de valores:

$$ \begin{array}{c|c} x & y & y/x \\ \hline -1 & -2 & 2 \\ 0 & 0 & - \\ 1 & 2 & 2 \\ 2 & 4 & 2 \\ 3 & 6 & 2 \end{array} $$

Comprobemos ahora si la función cumple con las condiciones de proporcionalidad directa:

• Para cualquier valor distinto de cero de x (x≠0), la razón y/x se mantiene constante e igual a 2.
• La gráfica de la función pasa por el origen (0,0).

Se verifican ambas condiciones.

Por lo tanto, la función y=2x es una función directamente proporcional.

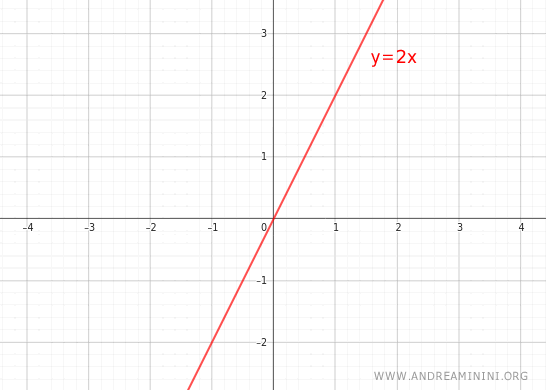
Nota. En este caso, la razón es 1:2, ya que la variable y crece al doble de la velocidad de x.

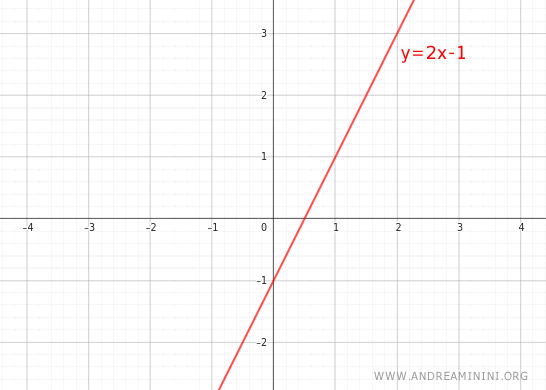
Ejemplo 2

Consideremos ahora la función:

$$ y=2x-1 $$

La tabla de valores correspondiente es la siguiente:

$$ \begin{array}{c|c} x & y & y/x \\ \hline -1 & -3 & 3 \\ 0 & \color{red}{-1} & - \\ 1 & 1 & 1 \\ 2 & 3 & 1.5 \\ 3 & 5 & 1.66 \end{array} $$

En este caso, aunque la gráfica es una línea recta, la función no es directamente proporcional porque no pasa por el origen (0,0).

Además, la razón k=y/x no permanece constante.

Y así sucesivamente...