Función signo
¿Qué es la función signo?
- En matemáticas, la función signo, representada como Sgn(x), se define de la siguiente manera: $$ Sgn(x) = \frac{x}{|x|} $$ Sus valores son:
- $f(x) = 1$ si $x > 0$
- $f(x) = -1$ si $x < 0$
Recibe este nombre porque indica el signo del número de entrada $x$.
A continuación se muestra la gráfica de Sgn(x):
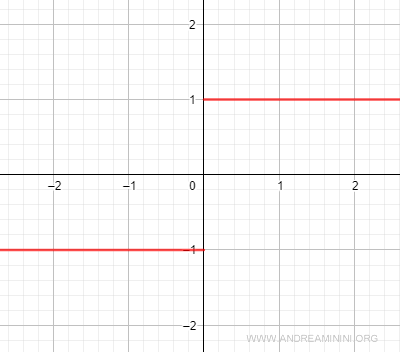
En $x=0$ la función no está definida, ya que el origen constituye un punto de discontinuidad.
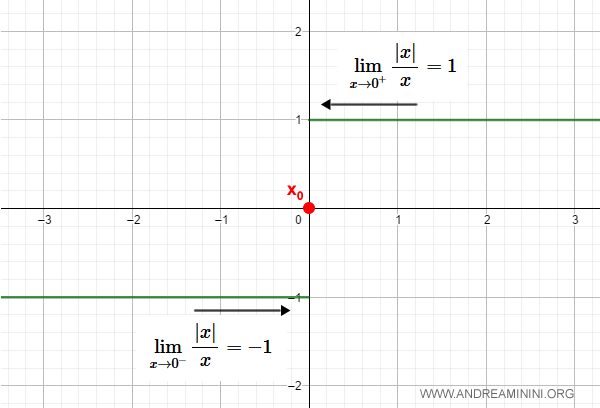
De hecho, los límites laterales al aproximarse $x$ a cero son distintos:
$$ \lim_{x \rightarrow 0^-} Sgn(x) = -1 $$
$$ \lim_{x \rightarrow 0^+} Sgn(x) = +1 $$
Este salto de $-1$ a $+1$ provoca una discontinuidad en el origen.
Desde el punto de vista matemático, se trata de una discontinuidad de primera especie. Por convención, a menudo se asigna $f(0)=0$, que corresponde al punto medio entre los dos límites laterales.
Y así sucesivamente.