Intervalos

En matemáticas, un intervalo es un conjunto de números reales consecutivos delimitado por un extremo inferior (a) y/o un extremo superior (b), con a< b.

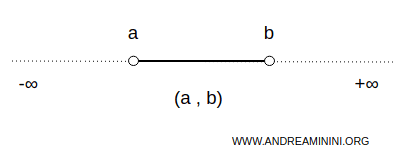
Un intervalo se denomina cerrado cuando incluye sus extremos, y abierto cuando los excluye.

Puede estar limitado por dos extremos finitos o extenderse indefinidamente en una o en ambas direcciones.

La diferencia entre los extremos define la longitud del intervalo.

$$ b - a $$

El centro del intervalo corresponde al punto medio entre los extremos:

$$ \frac{a+b}{2} $$

El radio del intervalo es la mitad de su longitud:

$$ \frac{b-a}{2} $$

Nota. En la notación matemática habitual, un intervalo con extremos "a" y "b" se escribe con una coma, como en (a,b). Sin embargo, dado que en Italia la coma se utiliza como separador decimal, en algunos contextos se emplea el punto y coma, es decir, (a;b). Por ejemplo, si los extremos son los decimales 2,5 y 3,4, escribir (2,5,3,4) resultaría ambiguo. En estos casos, se recomienda usar el punto decimal (2.5,3.4) o bien el punto y coma como separador (2.5;3.4).

Diferencia entre intervalos acotados y no acotados

Según la presencia o ausencia de extremos finitos, los intervalos se clasifican en acotados y no acotados.

• Intervalo acotado
  Un intervalo acotado es un conjunto de números comprendidos entre dos valores, un extremo inferior (a) y un extremo superior (b), con a< b.
  

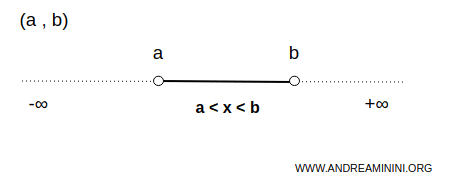
  Ejemplo. El conjunto de los números reales comprendidos entre 3 y 10 forma un intervalo acotado, donde 3 es el extremo inferior y 10 el extremo superior. $$ \forall \ x \in (3,10) \Rightarrow \forall \ x \in R \ | \ 3 \lt x \ \lt 10 $$

• Intervalo no acotado
  Un intervalo no acotado es un conjunto de números que se extiende indefinidamente hacia la derecha o hacia la izquierda a partir de un valor dado.
  
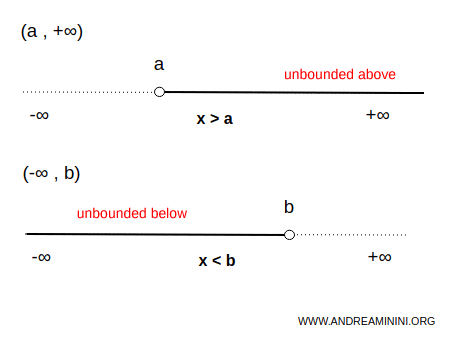
  Los símbolos $ - \infty $ y $ + \infty $ no representan números reales, por lo que nunca pueden formar parte de un intervalo.
  

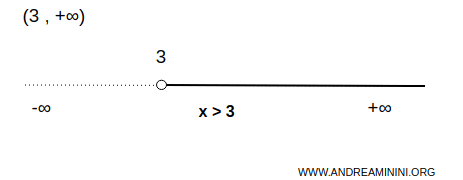
  Ejemplo. El conjunto de los números reales mayores que 3 es un intervalo no acotado superiormente y acotado inferiormente. El valor 3 es el extremo inferior, mientras que no existe un extremo superior. $$ \forall \ x \in (3,+\infty) \Rightarrow \forall \ x \in R \ | \ x \ \gt 3 $$
  
  Ejemplo. El conjunto de los números reales menores que 3 es un intervalo no acotado inferiormente y acotado superiormente. En este caso, 3 es el extremo superior. $$ \forall \ x \in (-\infty,3) \Rightarrow \forall \ x \in R \ | \ x \ \lt 3 $$
  

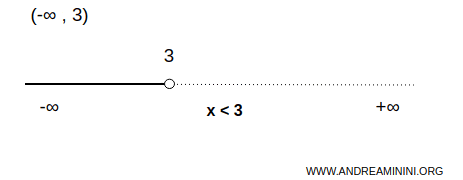
Intervalos no acotados en ambas direcciones

Cuando un intervalo no está acotado ni por abajo ni por arriba, incluye todos los elementos del conjunto numérico considerado.

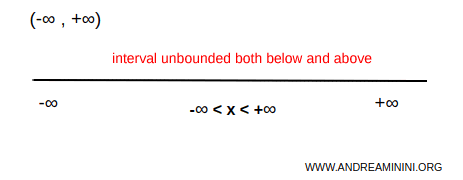
En este caso, se habla simplemente de un intervalo no acotado.

Ejemplo. El conjunto de los números reales (R) es un intervalo no acotado que se extiende indefinidamente en ambas direcciones e incluye todos los números reales. $$ \forall \ x \in (-\infty,+\infty) \Rightarrow \forall \ x \ \in R $$

Intervalos abiertos y cerrados

Según la inclusión o exclusión de sus extremos, un intervalo puede ser abierto o cerrado.

• Intervalo cerrado
  Un intervalo es cerrado cuando incluye sus extremos. Se representa con corchetes [ ]. En una representación gráfica, los extremos cerrados se muestran como puntos rellenos.
  
  

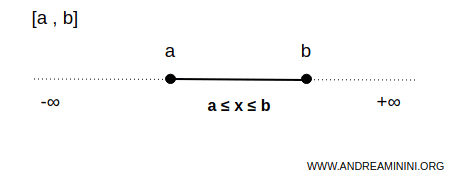
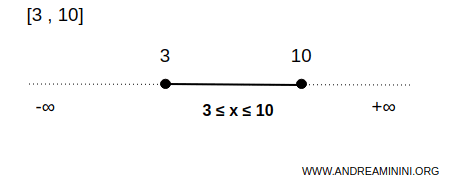
  Ejemplo. El intervalo $$ x \in [3,10] $$ incluye todos los números entre 3 y 10, incluidos ambos extremos.
  

• Intervalo abierto
  Un intervalo es abierto cuando no incluye sus extremos. Se representa con paréntesis ( ). En los gráficos, los extremos abiertos aparecen como puntos huecos.
  
  

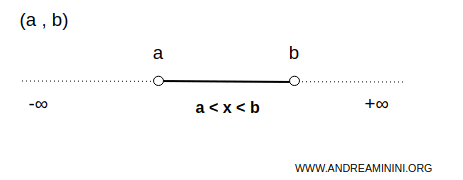
  Ejemplo. El intervalo $$ x \in (3,10) $$ contiene todos los números comprendidos entre 3 y 10, excluyendo ambos extremos.
  

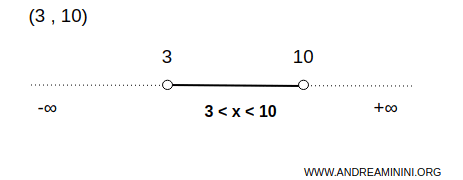
Existen muchas combinaciones posibles de intervalos, según cómo se incluyan o excluyan los extremos y si el intervalo es acotado o no.

Nota. En algunos manuales se utiliza la notación alternativa $$ ]a,b[ \ = (a,b) $$ para los intervalos abiertos. El significado matemático es el mismo, aunque aquí se prefiere el uso de paréntesis.

Ejemplos prácticos

Ejemplo 1

Intervalo acotado, abierto por la izquierda y cerrado por la derecha:

$$ x \in (3,10] $$

Incluye todos los números entre 3 y 10, excluyendo 3 e incluyendo 10.

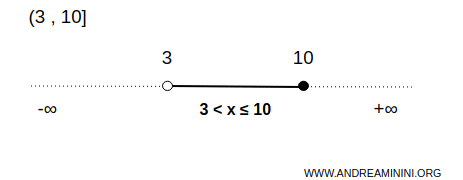
Ejemplo 2

Intervalo acotado, cerrado por la izquierda y abierto por la derecha:

$$ x \in [3,10) $$

Incluye todos los números entre 3 y 10, incluyendo 3 y excluyendo 10.

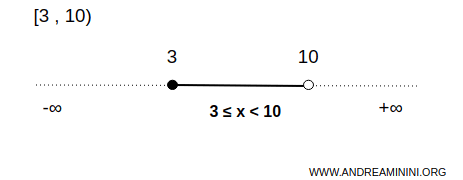
Ejemplo 3

Intervalo no acotado superiormente y cerrado por la izquierda:

$$ x \in [3,+\infty) \Rightarrow \forall \ x \ge 3 $$

Incluye todos los números mayores o iguales que 3.

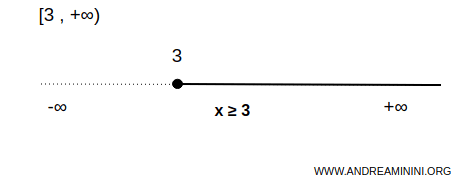
Nota. Los extremos infinitos nunca se incluyen en un intervalo, ya que ±∞ no es un número real. Por esta razón, en los extremos no acotados siempre se utilizan paréntesis.

Ejemplo 4

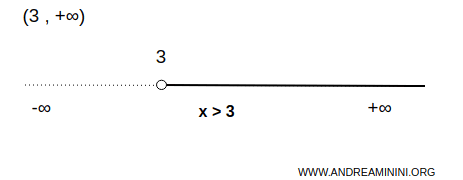
Intervalo no acotado superiormente y abierto en ambos extremos:

$$ x \in (3,+\infty) \Rightarrow \forall \ x \gt 3 $$

Ejemplo 5

Intervalo no acotado inferiormente, abierto por la izquierda y cerrado por la derecha:

$$ x \in (-\infty,10] \Rightarrow \forall \ x \le 10 $$

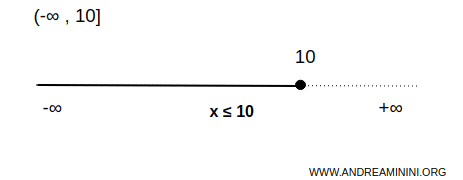
Ejemplo 6

Intervalo no acotado inferiormente y abierto en ambos extremos:

$$ x \in (-\infty, 10) \Rightarrow \forall \ x \lt 10 $$

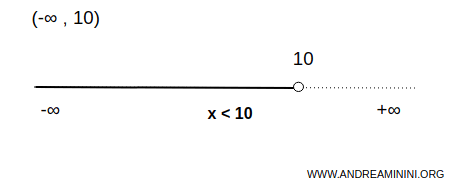
Y así sucesivamente.