Funciones sobreyectivas

¿Qué es una función sobreyectiva?

Una función se denomina sobreyectiva (o “sobre”) cuando cada elemento del codominio es imagen de al menos un elemento del dominio: $$ \forall \: y, \: \exists \: x \text{ tal que } f(x) = y $$

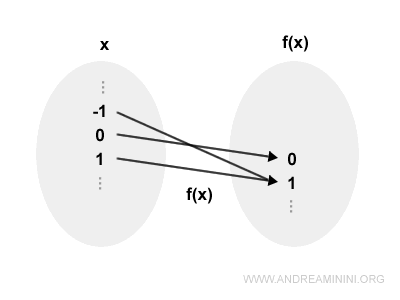
Los diagramas de Venn proporcionan una representación visual especialmente clara de la sobreyectividad.

En una función sobreyectiva, cada elemento del codominio (B) está “cubierto”: es decir, existe al menos un valor de entrada en el dominio (A) que lo genera.

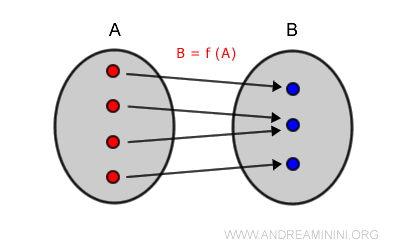
example of a surjective function

De manera formal, una función $f$ es sobreyectiva si:

$$ \forall \ y \in B, \ \exists \ x \in A \text{ tal que } f(x) = y $$

Nota. No es necesario que a cada $y \in B$ le corresponda un único $x \in A$; distintos valores de entrada pueden compartir la misma imagen. Lo esencial es que todos los elementos del codominio sean alcanzados por algún elemento del dominio.

En otras palabras, cada elemento de $B$ (el codominio) posee al menos una preimagen en $A$ (el dominio).

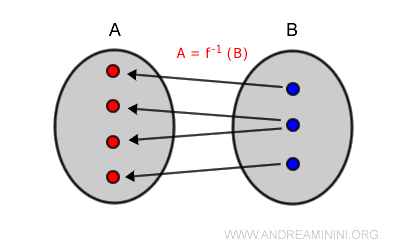
visual representation of a surjective function

Cuando una función es sobreyectiva, el conjunto objetivo $B$ coincide exactamente con su codominio.

De este modo, la sobreyectividad depende directamente de cómo se defina el codominio.

Nota. Cualquier función puede hacerse sobreyectiva si se restringe su codominio a su imagen, es decir, al conjunto de valores que efectivamente alcanza. Por ejemplo, la función $f(x) = 2x$ no es sobreyectiva si el codominio incluye el número 10, ya que 10 no es el doble de ningún elemento de $A$.
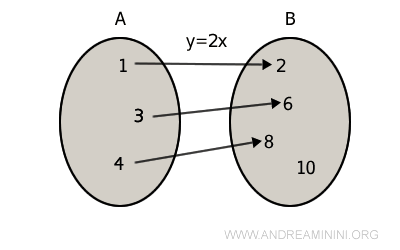
function that is not surjective onto B
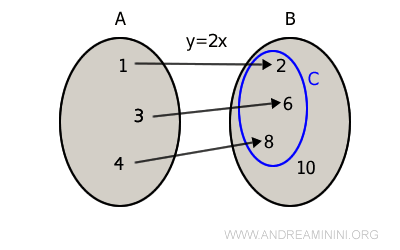
No obstante, si redefinimos el codominio como la imagen $C = \{2, 6, 8\}$, entonces $f(x) = 2x$ pasa a ser sobreyectiva.
function becomes surjective by redefining the codomain

Ejemplo

Consideremos una función que resulta sobreyectiva en el intervalo $y \in [a, b]$, ya que cada valor de $y$ en ese intervalo posee al menos una preimagen $x$.

graph of a surjective function on [a, b]

En cambio, la misma función no es sobreyectiva en $y \in [0, b]$, pues los valores de $[0, a]$ no son alcanzados por ningún $x$.

Para garantizar la sobreyectividad basta restringir el codominio a la imagen de la función, es decir, a $[a, b]$ en lugar de $[0, b]$.

Una vez ajustado el codominio a la imagen real, la función se convierte en sobreyectiva.

Un ejemplo práctico

Ejemplo 1

Sea el dominio y el codominio ambos el conjunto de los números reales $\mathbb{R}$:

$$ f: \mathbb{R} \rightarrow \mathbb{R} $$

La función

$$ f(x) = x + 1 $$

es sobreyectiva, ya que cualquier número real $y$ puede escribirse como $f(x)$ para algún $x \in \mathbb{R}$.

x	y = f(x)
-3	-2
-2	-1
-1	0
0	1
1	2
2	3
3	4

Cada valor de salida $y$ está asociado con al menos una entrada $x$.

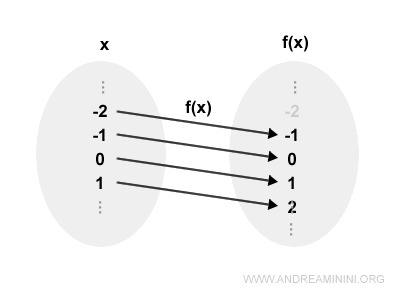
table showing surjectivity of f(x) = x + 1

Por lo tanto, $f(x) = x + 1$ es sobreyectiva en el conjunto de los números reales.

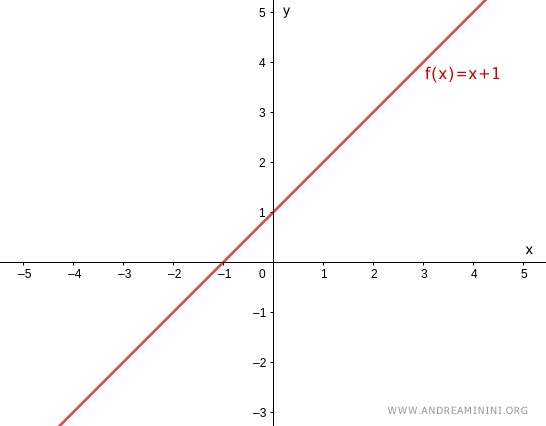
graph of a surjective function over ℝ

Ejemplo 2

De nuevo, sea el dominio y el codominio $\mathbb{R}$:

$$ f: \mathbb{R} \rightarrow \mathbb{R} $$

La función

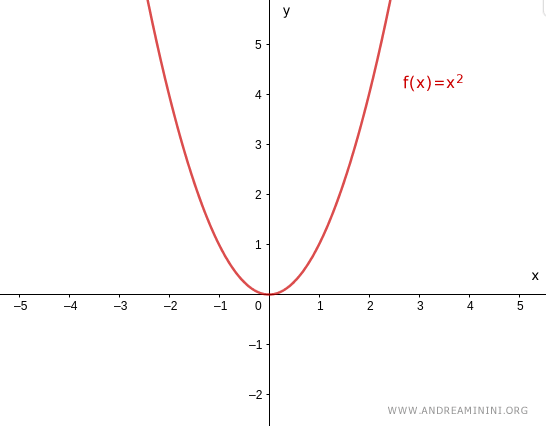
$$ f(x) = x^2 $$

no es sobreyectiva, porque ciertos valores del codominio $\mathbb{R}$ - como los números negativos - no pueden obtenerse a partir de ningún valor real de entrada.

x	y = f(x)
-3	9
-2	4
-1	1
0	0
1	1
2	4
3	9

Por ejemplo, no existe ningún $x$ tal que $x^2 = -2$ o $x^2 = -3$.

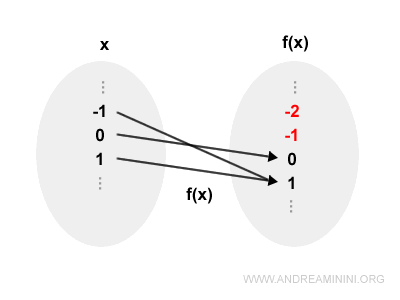
table showing function f(x) = x² is not surjective

En consecuencia, $f(x) = x^2$ no es sobreyectiva si el codominio es $\mathbb{R}$.

graph of f(x) = x² showing non-surjectivity on ℝ

Nota. Para que $f(x) = x^2$ sea sobreyectiva, basta redefinir el codominio como el conjunto de los números reales no negativos: $$ f: \mathbb{R} \rightarrow \mathbb{R}^+ \cup \{0\} $$ Con esta elección, todo $y \ge 0$ en el codominio tiene al menos una preimagen en el dominio.
graph showing f(x) = x² is surjective on ℝ⁺ ∪ {0}

Y así sucesivamente.