Cómo analizar una función

El análisis de una función f(x) permite esbozar su gráfica a partir del estudio de su dominio, el signo y las derivadas primera y segunda.

Consideremos como ejemplo la siguiente función:

$$ f(x)= \frac{x}{x-1} $$

Para representar su gráfica, seguiremos una serie de pasos ordenados:

Determinación del dominio

El primer paso es identificar el dominio, es decir, el conjunto de valores de x para los cuales la función está definida.

En nuestro caso, f(x) = x / (x - 1) tiene dominio:

$$ ( -\infty, 1) \cup (1, \infty ) \:\:\:\: \forall x \in \mathbb{R} $$

Esto pone de relieve los puntos donde la función no está definida.

En particular, f(x) = x / (x - 1) no está definida en x = 1:

$$ f(1)= \frac{1}{1-1} |_{x=1} = \frac{1}{0} \:\:\: \text{indefinida} $$

Estos puntos suelen corresponder a asíntotas verticales.

Análisis del signo de la función

El siguiente paso consiste en determinar en qué intervalos la función toma valores positivos o negativos.

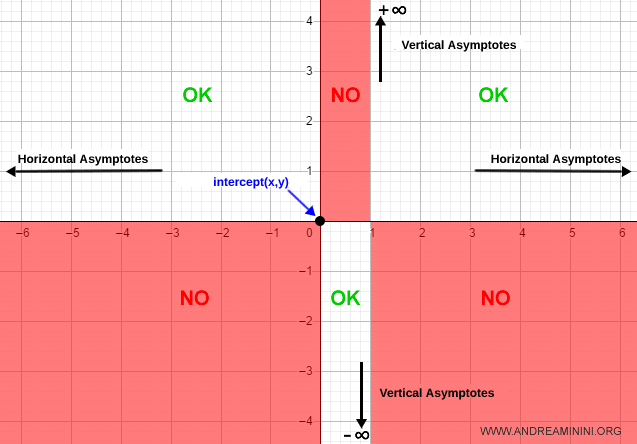
Aquí, la función es positiva en los intervalos (-\infty, 0) y (1, \infty), y negativa en (0, 1).

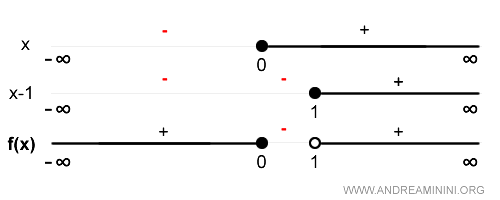
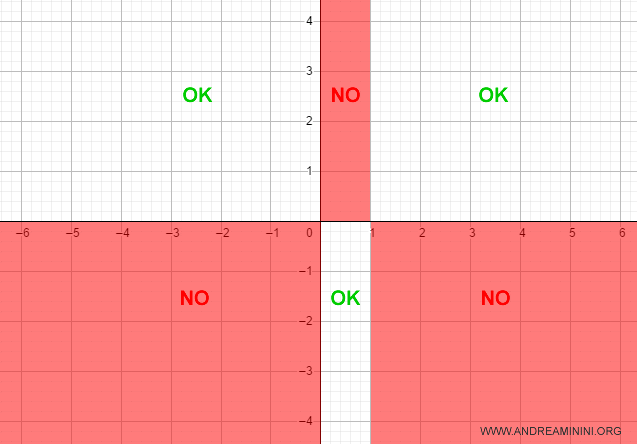
Este análisis indica en qué cuadrantes del plano cartesiano se sitúa la gráfica.

Los cuadrantes en los que no aparece pueden descartarse directamente.

Asíntotas horizontales

Para determinar las asíntotas horizontales calculamos los límites de la función cuando x tiende a infinito positivo y negativo, es decir, en los extremos de su dominio.

$$ \lim_{x \rightarrow \infty}{ \frac{x}{x-1} } = \frac{\infty}{\infty} $$

$$ \lim_{x \rightarrow -\infty}{ \frac{x}{x-1} } = \frac{\infty}{\infty} $$

Ambos casos son indeterminaciones.

Aplicamos la Regla de L'Hôpital para resolverlos:

$$ \lim_{x \rightarrow \infty}{ \frac{D[x]}{D[x-1]} } = \lim_{x \rightarrow \infty}{ \frac{1}{1} } = 1 $$

$$ \lim_{x \rightarrow -\infty}{ \frac{D[x]}{D[x-1]} } = \lim_{x \rightarrow -\infty}{ \frac{1}{1} } = 1 $$

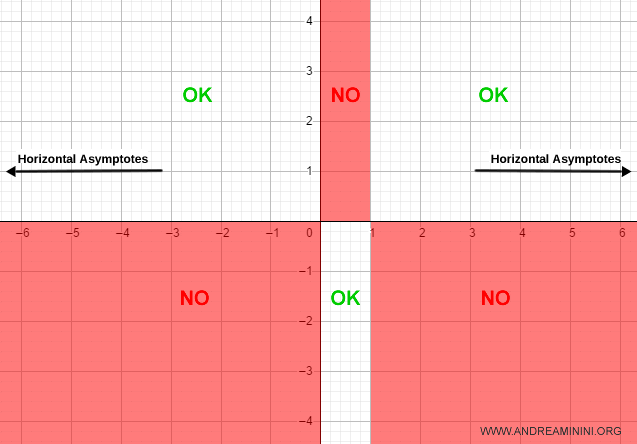
Como ambos límites son finitos, la función presenta dos asíntotas horizontales en y = 1 cuando x tiende a ±∞:

$$ \lim_{x \rightarrow \infty}{ \frac{x}{x-1} } = 1 $$

$$ \lim_{x \rightarrow -\infty}{ \frac{x}{x-1} } = 1 $$

Incorporamos ahora estas asíntotas al gráfico:

Asíntotas verticales

En los puntos de no definición conviene calcular los límites laterales, aproximándose desde la izquierda y la derecha.

En este caso, la función no está definida en x = 1:

$$ \lim_{x \rightarrow 1^+}{ \frac{x}{x-1} } = \frac{1}{0^+} = \infty $$

$$ \lim_{x \rightarrow 1^-}{ \frac{x}{x-1} } = \frac{1}{0^-} = -\infty $$

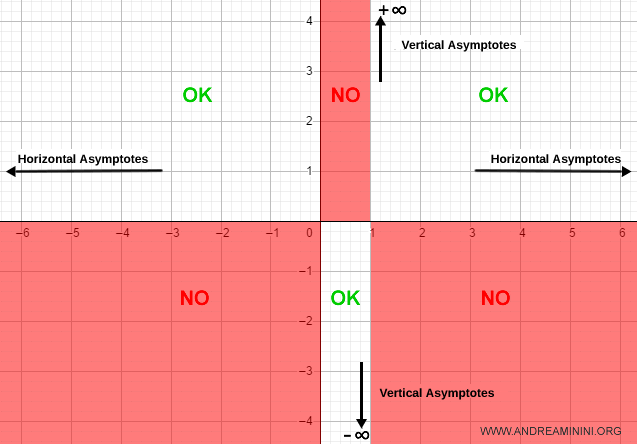
Así, cuando x se aproxima a 1 por la derecha, la función tiende a +∞; y por la izquierda, a -∞.

Añadimos la asíntota vertical al gráfico:

Asíntotas oblicuas

Si x tiende a ±∞, comprobamos si existe una asíntota oblicua de la forma y = mx + q evaluando:

$$ m = \lim_{x \rightarrow \infty } \frac{f(x)}{x} =\lim_{x \rightarrow \infty } \frac{\frac{x}{x-1}}{x} = 0 $$

$$ q = \lim_{x \rightarrow \infty } [f(x) - mx] = \lim_{x \rightarrow \infty } \left( \frac{x}{x-1} - 0 \cdot x \right) = 1 $$

Si estos límites existen, son finitos y m ≠ 0, existe una asíntota oblicua de la forma mx + q.

En este caso, como m = 0, no hay asíntota oblicua cuando x → ±∞.

Nota. Para esta función, la pendiente m = 0 y q = 1, lo cual coincide con la asíntota horizontal ya encontrada. Por tanto, no hay asíntotas oblicuas.

Análisis de simetría

Conviene examinar si la función presenta algún tipo de simetría.

Por ejemplo, si es par:

$$ f(-x) = f(x) $$

o impar:

$$ f(-x) = -f(x) $$

En este caso, la función x / (x - 1) no presenta simetría alguna.

Periodicidad

Después verificamos si la función es periódica con periodo T:

$$ T: f(x+T) = f(x) \:\:\:\: \forall x \in \mathbb{R} $$

Un ejemplo clásico es la función seno, periódica con periodo T = 2π.

Si la función fuera periódica, bastaría estudiar un único periodo y extender los resultados a los siguientes intervalos.

En nuestro caso, la función x / (x - 1) no es periódica.

Intersecciones con los ejes

Los puntos de corte con los ejes proporcionan información adicional para construir la gráfica.

Corte con el eje y

Si fijamos x = 0, obtenemos el valor correspondiente de y:

$$ y = \frac{x}{x-1}|_{x=0} = \frac{0}{0-1} = 0 $$

La función corta el eje y en el origen (0, 0).

Corte con el eje x

También podemos calcular el corte con el eje x imponiendo y = 0:

$$ \frac{x}{x-1} = 0 $$

Nota. En este caso, el corte con el eje x coincide con el del eje y en el origen (0, 0). No siempre ocurre así: en otras funciones ambos cortes pueden ser distintos o incluso inexistentes.

Por lo tanto, la función pasa por el punto P(0, 0).

Intervalos de crecimiento y decrecimiento

Para determinar dónde la función crece o decrece, calculamos su primera derivada:

$$ f'(x) = D\left[ \frac{x}{x-1} \right] = \frac{(x-1)-x}{(x-1)^2} = \frac{-1}{(x-1)^2} $$

A continuación se analiza el signo de la derivada primera:

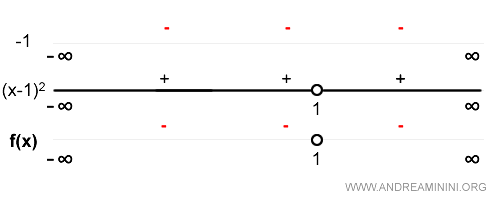
La función es creciente cuando f'(x) > 0 y decreciente cuando f'(x) < 0.

En este caso, resulta decreciente en todo su dominio.

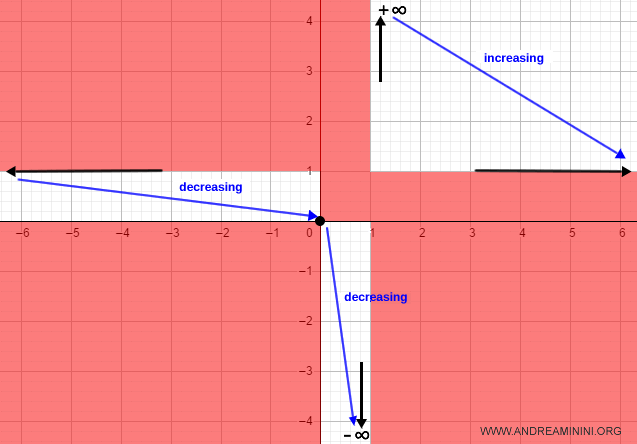
En el intervalo (-\infty, 0), la función desciende desde la asíntota horizontal y = 1 hasta el origen.

En (0, 1), pasa por el origen y decrece hacia -∞.

En (1, \infty), desciende desde la asíntota vertical hasta la horizontal en y = 1.

Nota. Estas conclusiones permiten descartar directamente las regiones del plano cartesiano en las que la función no puede representarse.

Mínimos y máximos locales

El siguiente paso consiste en localizar los puntos críticos x₀ en los que la primera derivada se anula, con el objetivo de identificar posibles extremos locales:

$$ f'(x_0) = 0 $$

En tales puntos se cumple:

• Máximo local: si la función crece a la izquierda de x₀ ( f'(x) > 0 ) y decrece a la derecha ( f'(x) < 0 ).
• Mínimo local: si la función decrece a la izquierda de x₀ ( f'(x) < 0 ) y crece a la derecha ( f'(x) > 0 ).

En cualquier otro caso, la función no presenta ni mínimo ni máximo local en x₀.

En esta función, la primera derivada nunca se anula:

$$ f'(x) = \frac{-1}{(x-1)^2} \ne 0 \:\:\:\: \forall x \in \mathbb{R} $$

Por consiguiente, no existen mínimos ni máximos locales en el dominio.

Puntos de inflexión

Se comprueba también la posible existencia de puntos de inflexión, que aparecen cuando la primera derivada se anula:

$$ f'(x_0) = 0 $$

Un punto de inflexión se produce si la función mantiene la misma monotonía a ambos lados de x₀, pero cambia su concavidad.

Para distinguir si se trata de una inflexión ascendente o descendente, se calcula la segunda derivada:

Si:

$$ f''(x_0) = 0 $$

Entonces:

• Inflexión ascendente: si f''(x) pasa de negativa a positiva en torno a x₀ (de cóncava hacia abajo a cóncava hacia arriba).
• Inflexión descendente: si f''(x) pasa de positiva a negativa en torno a x₀ (de cóncava hacia arriba a cóncava hacia abajo).

En esta función, la primera derivada nunca se anula:

$$ f'(x) = \frac{-1}{(x-1)^2} \ne 0 \:\:\:\: \forall x \in \mathbb{R} $$

En consecuencia, no existen puntos de inflexión en el dominio.

Concavidad y convexidad

Finalmente, se calcula la segunda derivada para determinar los intervalos de concavidad y convexidad:

$$ D^2[ f(x) ] = D\left[ \frac{-1}{(x-1)^2} \right] = \frac{ 2(x-1)}{(x-1)^4} = \frac{2}{(x-1)^3} $$

Se analiza a continuación el signo de la segunda derivada:

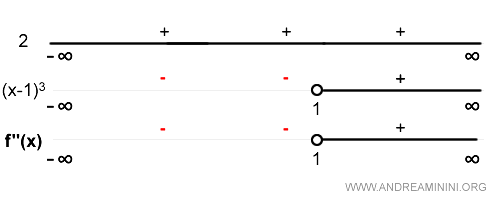
La función resulta:

• convexa cuando f''(x) > 0,
• cóncava cuando f''(x) < 0.

En consecuencia, la función f(x) = x / (x - 1) es cóncava en el intervalo (-\infty, 1) y convexa en (1, \infty).

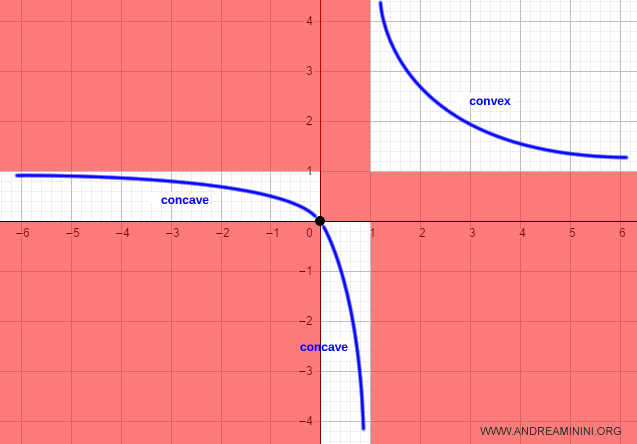
Con esto queda completado el estudio y la representación de la función.

Y así sucesivamente.