Ejemplo resuelto de análisis de funciones 2

Analicemos la gráfica de la siguiente función:

$$ f(x) = \frac{x-1}{x+1} $$

Dominio

La función está definida en:

$$ D_f = (-\infty, -1) \cup (-1, +\infty) \ \ \ \forall \ x \in \mathbb{R} $$

Análisis del signo

La función toma valores positivos en los intervalos $ (-\infty, -1) \cup (1, +\infty) $, y negativos en $ (-1, 1) $:

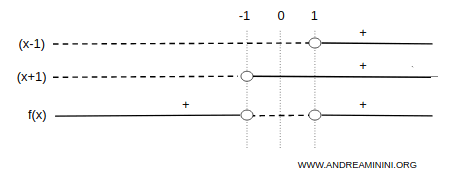
análisis del signo de la función

Esto permite descartar aquellas regiones del plano donde la función no adopta valores (zonas sombreadas en gris):

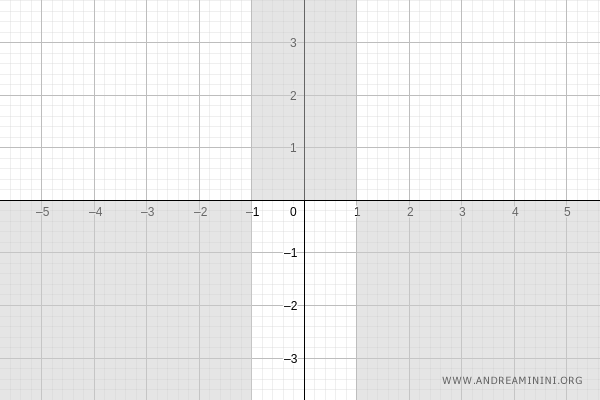
regiones donde la función está definida

Puntos de no definición

La función no está definida en $ x = -1 $, pues el denominador se anula en ese punto. En consecuencia, allí aparece una asíntota vertical:

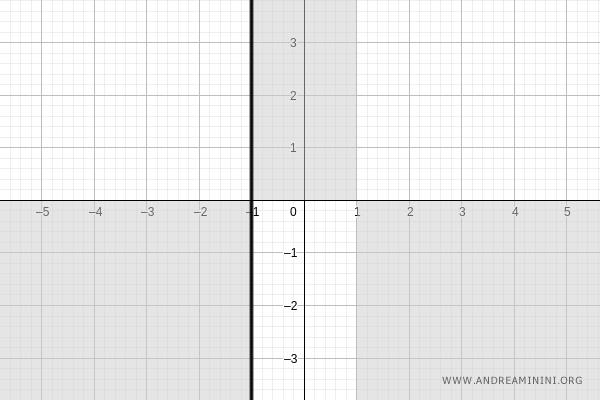
punto de no definición

Calculemos los límites laterales cuando $ x \to -1 $:

$$ \lim_{x \to -1^-} \frac{x-1}{x+1} = +\infty $$

$$ \lim_{x \to -1^+} \frac{x-1}{x+1} = -\infty $$

Así, al aproximarse a $ -1 $, la función tiende a $ +\infty $ por la izquierda y a $ -\infty $ por la derecha:

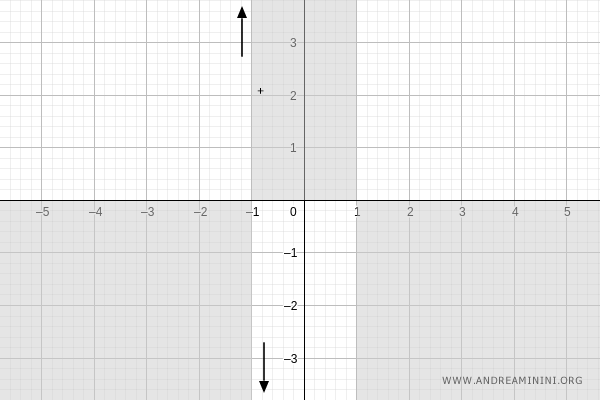
asíntota vertical en x = -1

Intersecciones con los ejes

Para $ x = 0 $:

$$ f(0) = \frac{0-1}{0+1} = -1 $$

La gráfica pasa por el punto $ (0, -1) $:

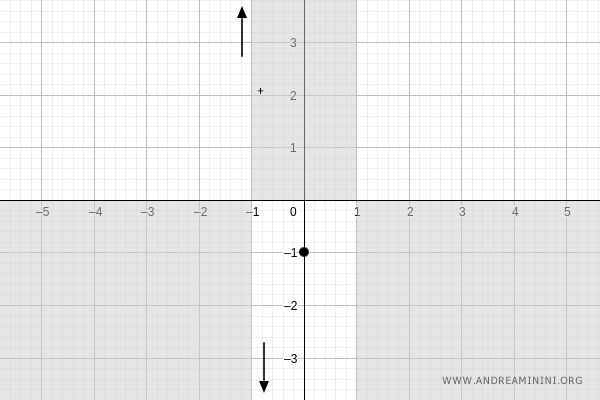
intersección en (0, -1)

Busquemos ahora la intersección con el eje x (cuando $ f(x) = 0 $):

$$ \frac{x-1}{x+1} = 0 $$

$$ x - 1 = 0 \quad \Rightarrow \quad x = 1 $$

Por tanto, la gráfica también pasa por $ (1, 0) $:

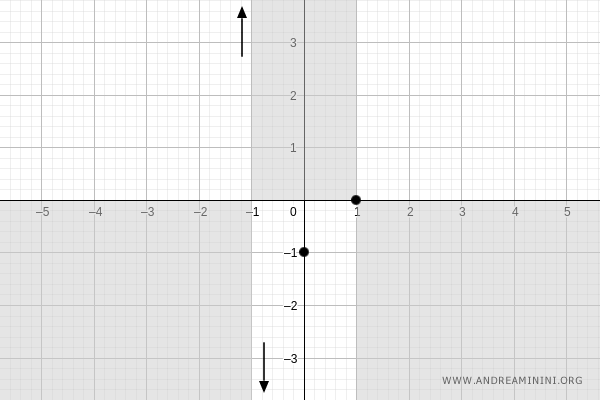
intersección en (1, 0)

Asíntotas horizontales

Calculemos el límite cuando $ x \to +\infty $:

$$ \lim_{x \to +\infty} \frac{x-1}{x+1} = \frac{\infty}{\infty} $$

Se trata de una forma indeterminada $ \tfrac{\infty}{\infty} $, por lo que aplicamos la regla de L'Hôpital:

$$ \lim_{x \to +\infty} \frac{D[x-1]}{D[x+1]} = \frac{1}{1} = 1 $$

En consecuencia, cuando $ x \to +\infty $, $ f(x) \to 1 $:

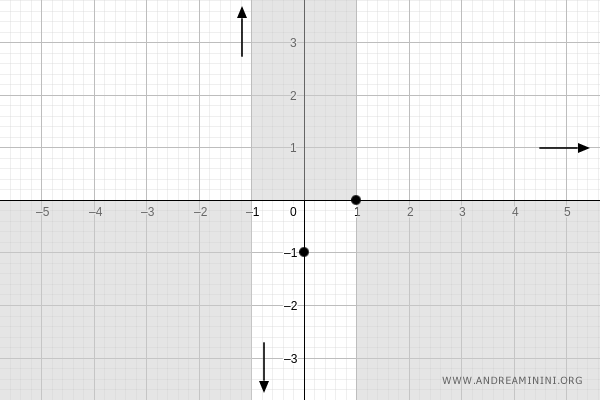
asíntota horizontal en y = 1

De manera análoga, cuando $ x \to -\infty $:

$$ \lim_{x \to -\infty} \frac{x-1}{x+1} = \frac{\infty}{\infty} $$

Aplicando nuevamente la regla de L'Hôpital:

$$ \lim_{x \to -\infty} \frac{D[x-1]}{D[x+1]} = \frac{1}{1} = 1 $$

Así, cuando $ x \to -\infty $, $ f(x) \to 1 $:

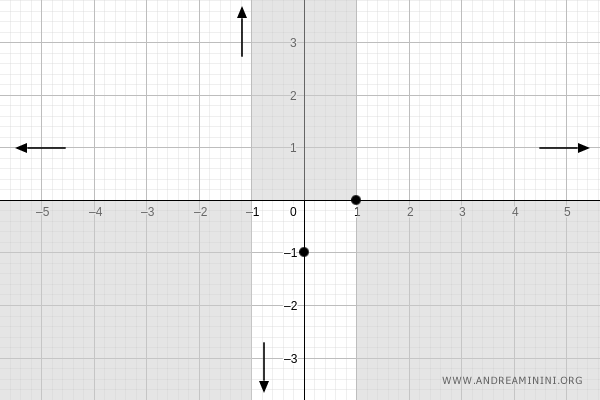
asíntota horizontal en y = 1 para x → -∞

Monotonía

Calculemos la primera derivada:

$$ f'(x) = D\left[\frac{x-1}{x+1}\right] = \frac{(x+1) - (x-1)}{(x+1)^2} = \frac{2}{(x+1)^2} $$

Como $ f'(x) > 0 $ para todo $ x \in D_f $, la función es estrictamente creciente:

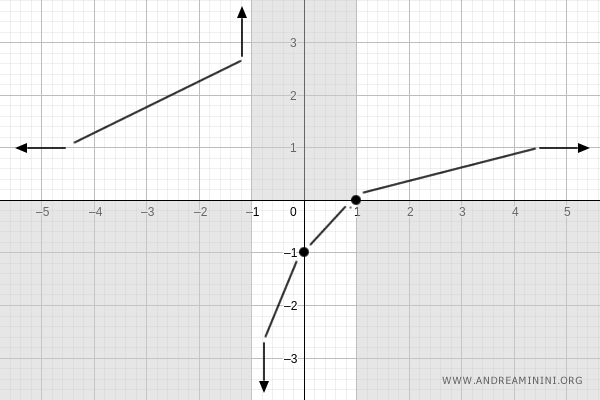
la función es creciente

Concavidad y convexidad

Calculamos ahora la segunda derivada:

$$ f''(x) = D\left[ \frac{2}{(x+1)^2} \right] = -4(x+1)^{-3} = \frac{-4}{(x+1)^3} $$

El signo de la segunda derivada es positivo en $ (-\infty, -1) $ y negativo en $ (-1, +\infty) $:

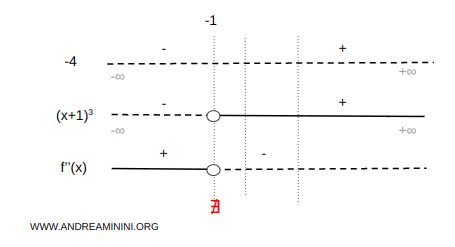
análisis del signo de la segunda derivada

En consecuencia:

La función es convexa en $ (-\infty, -1) $.
La función es cóncava en $ (-1, +\infty) $.

La gráfica se actualiza de acuerdo con este resultado:

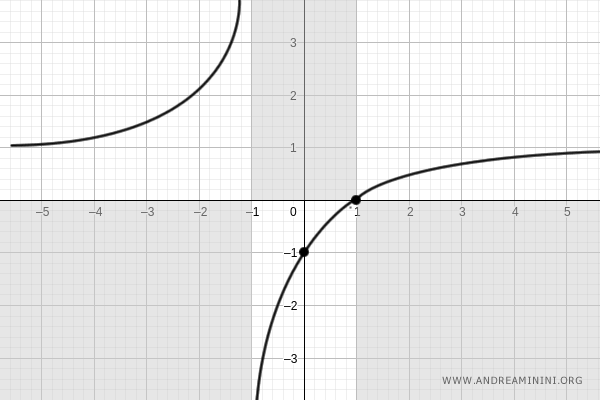
gráfica final de la función

Y así sucesivamente.