Ejemplo resuelto de análisis de funciones 1
En este ejemplo vamos a estudiar la siguiente función:
$$ f(x) = \frac{x+1}{x-1} $$
Comenzamos representando un plano cartesiano en blanco:
El primer paso es determinar el dominio de la función.
La función está definida para todos los números reales, excepto en $x = 1$:
$$ (-\infty, 1) \cup (1, +\infty) $$
A continuación calculamos las intersecciones de $f(x)$ con los ejes coordenados.
Para la intersección con el eje $y$, fijamos $x = 0$:
$$ f(0) = \frac{0+1}{0-1} = -1 $$
Por tanto, la gráfica pasa por el punto $(0, -1)$:
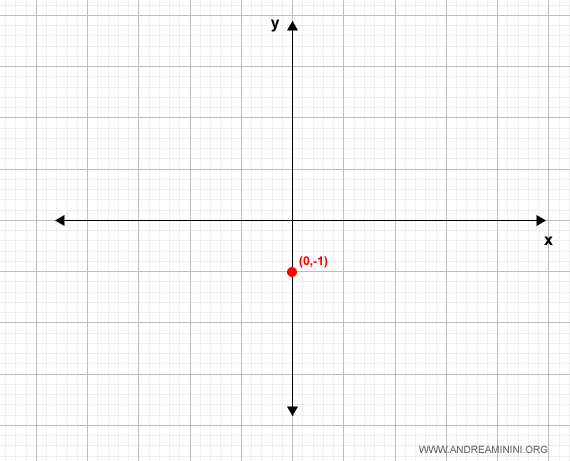
Para encontrar la intersección con el eje $x$, resolvemos:
$$ \frac{x+1}{x-1} = 0 $$
La solución es $x = -1$, de modo que la gráfica también pasa por $(-1, 0)$:
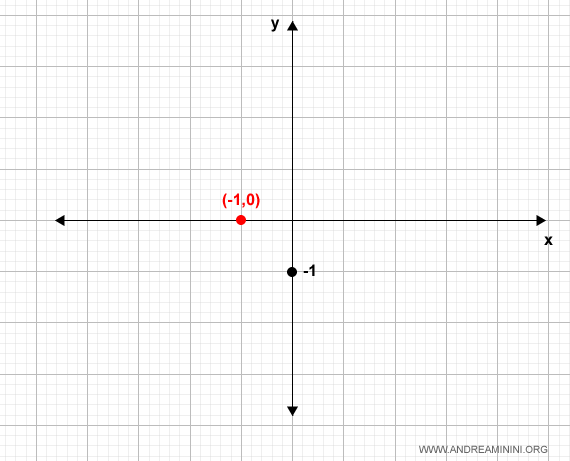
Analicemos ahora el comportamiento de $f(x)$ cuando $x$ tiende a $\pm\infty$:
$$ \lim_{x \rightarrow +\infty} \frac{x+1}{x-1} = \frac{\infty}{\infty} $$
$$ \lim_{x \rightarrow -\infty} \frac{x+1}{x-1} = \frac{\infty}{\infty} $$
Ambos límites presentan una forma indeterminada del tipo ∞/∞. Aplicamos la regla de L'Hôpital:
$$ \lim_{x \rightarrow +\infty} \frac{x+1}{x-1} = 1 $$
$$ \lim_{x \rightarrow -\infty} \frac{x+1}{x-1} = 1 $$
La gráfica se ajusta para reflejar este comportamiento asintótico:
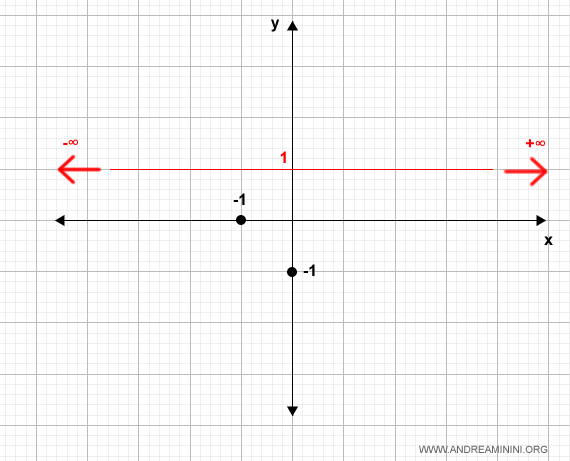
Examinemos ahora los puntos de indefinición.
El denominador se anula en $x = 1$, por lo que:
$$ f(1) = \frac{1+1}{1-1} = \frac{2}{0} $$
Esto señala la existencia de una asíntota vertical en $x = 1$.
Calculemos los límites laterales cuando $x$ se aproxima a 1:
$$ \lim_{x \rightarrow 1^+} \frac{x+1}{x-1} = +\infty $$
$$ \lim_{x \rightarrow 1^-} \frac{x+1}{x-1} = -\infty $$
Por lo tanto, al acercarse a $x = 1$, la función tiende a $-\infty$ por la izquierda y a $+\infty$ por la derecha. Representamos esta situación en la gráfica:
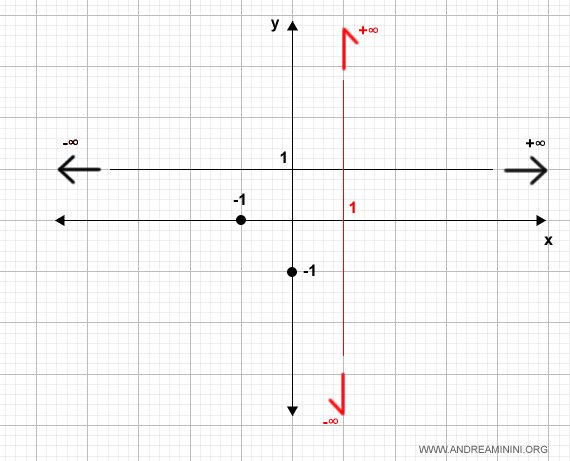
Procedamos ahora al análisis del signo de la función en su dominio:
$$ (-\infty, 1) \cup (1, +\infty) $$
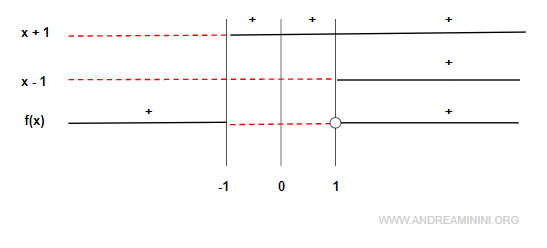
La función resulta positiva en $(-\infty, -1)$ y en $(1, +\infty)$, y negativa en $(-1, 1)$.
Podemos excluir las regiones del plano donde la función no tiene valores (zonas grises):
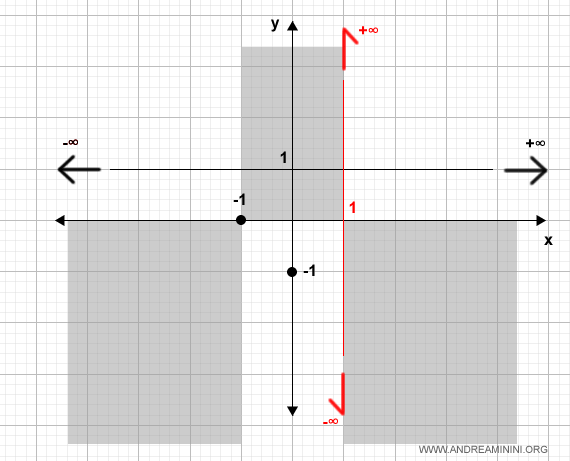
Calculamos ahora la primera derivada de la función:
$$ f'(x) = \frac{(x-1) - (x+1)}{(x-1)^2} = \frac{-2}{(x-1)^2} $$
Estudiamos el signo de $f'(x)$ en el dominio $(-\infty, 1) \cup (1, +\infty)$ para determinar los intervalos de crecimiento y decrecimiento:
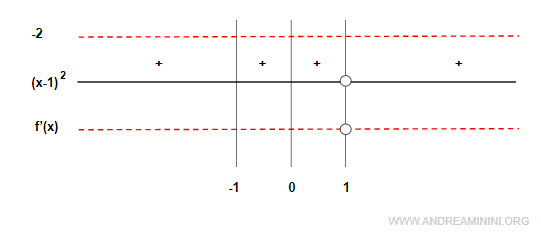
Dado que $f'(x) < 0$ en todo el dominio, la función es estrictamente decreciente.
Podemos esbozar ahora la curva de $f(x)$ uniendo los puntos obtenidos:
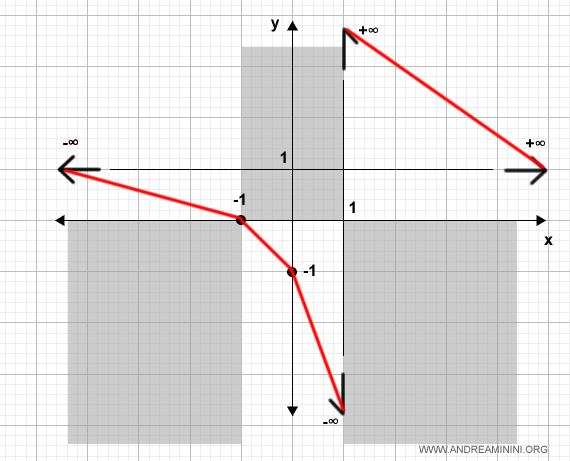
Calculamos a continuación la segunda derivada de la función:
$$ f''(x) = \frac{0 - (-2)(2(x-1))}{(x-1)^4} = \frac{4(x-1)}{(x-1)^4} = \frac{4}{(1-x)^3} $$
Analizamos el signo de $f''(x)$ en el dominio $(-\infty, 1) \cup (1, +\infty)$ para estudiar la concavidad y la convexidad:
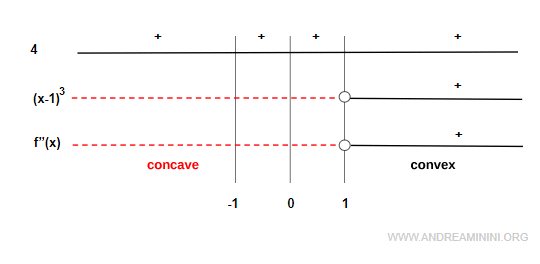
La función es cóncava en $(-\infty, 1)$, donde $f''(x) < 0$, y convexa en $(1, +\infty)$, donde $f''(x) > 0$.
La gráfica definitiva, que reúne toda la información obtenida, es la siguiente:
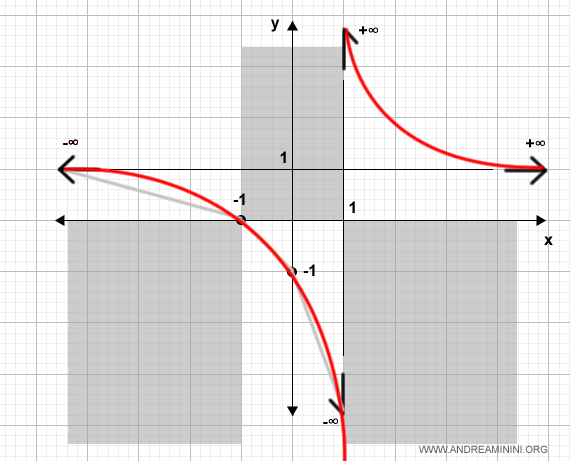
Con esto hemos completado el análisis integral de la función.
La representación gráfica final queda así:
Verificación. Gráfica de la función generada con GeoGebra:
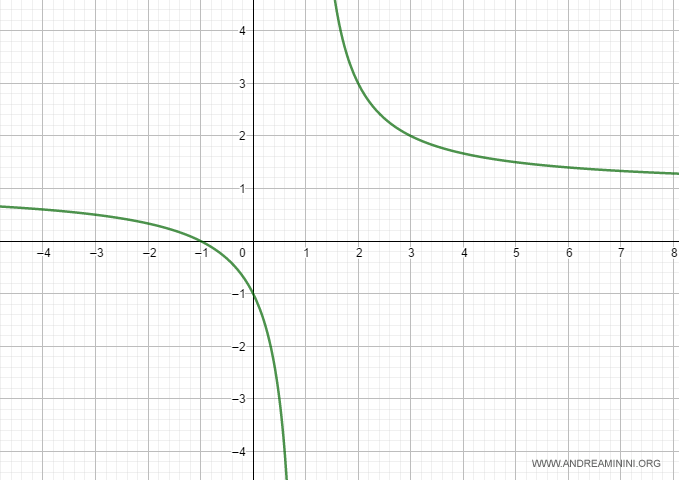
Y así sucesivamente.