Mínimos y máximos de una función

De acuerdo con el teorema de Fermat, si una función está definida en el intervalo [a, b] y alcanza un mínimo o un máximo local en un punto \( x₀ \), entonces su primera derivada en ese punto debe anularse: $$ f'(x_0)=0 $$

Por consiguiente, para determinar los mínimos y máximos locales seguimos este procedimiento:

1. Calcular la primera derivada de la función \( f(x) \).
2. Resolver la ecuación \( f'(x)=0 \) para hallar los puntos críticos.

Este método es válido únicamente si la función es derivable en todo el intervalo [a, b].

Una vez localizados los puntos donde la derivada se anula -denotémoslos por \( x₀ \)- debemos decidir si corresponden a un mínimo o a un máximo.

Cómo distinguir entre máximo y mínimo

Existen varios criterios posibles:

1. Estudiar el comportamiento de la primera derivada \( f'(x) \) alrededor de \( x₀ \).
   • Si la derivada crece en las cercanías de \( x₀ \), el punto corresponde a un mínimo local.
   • Si la derivada decrece en ese entorno, se trata de un máximo local.
2. Calcular la segunda derivada \( f''(x) \) en \( x₀ \).
   • Si la segunda derivada es positiva o nula, el punto es un mínimo local. $$ f''(x_0) \ge 0 \;\;\Leftrightarrow\;\; \text{mínimo} $$
   • Si la segunda derivada es negativa o nula, el punto es un máximo local. $$ f''(x_0) \le 0 \;\;\Leftrightarrow\;\; \text{máximo} $$

Nota. El criterio de la derivada también puede extenderse a derivadas sucesivas de orden par, siempre que todas las derivadas de orden inferior se anulen: $$ f^{(k)} \ne 0 \quad \text{para algún orden par } k $$ $$ f^{(1)} = f^{(2)} = \ldots = f^{(k-1)} = 0 $$ Este procedimiento constituye una herramienta poderosa en el análisis matemático y en el estudio de curvas, aunque requiere que la función sea continua y derivable en \( x₀ \).

Ambos criterios son equivalentes, gracias al criterio de monotonicidad:

• Si la primera derivada \( f'(x) \) es creciente alrededor de \( x₀ \), entonces necesariamente \( f''(x_0) \ge 0 \).
• Si la primera derivada \( f'(x) \) es decreciente cerca de \( x₀ \), entonces \( f''(x_0) \le 0 \).

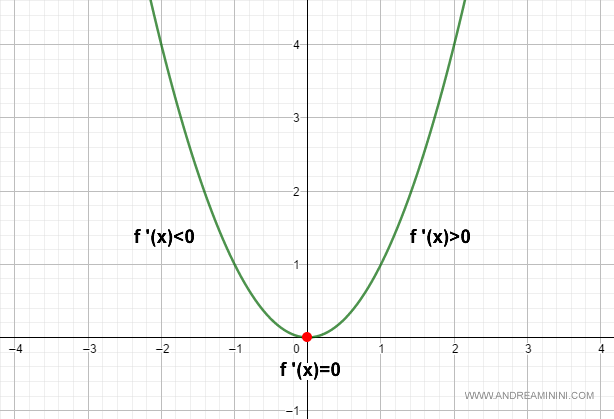
Un ejemplo práctico

Veamos ahora los extremos de la función:

$$ f(x)=x^2 $$

En primer lugar, calculamos la primera derivada:

$$ f'(x)=2x $$

Identificamos los puntos donde la derivada se anula:

La única solución es \( x=0 \):

$$ x=0 \;\;\Rightarrow\;\; f'(0)=0 $$

A continuación, calculamos la segunda derivada, es decir, la derivada de la primera derivada:

$$ f''(x)=2 $$

Evaluando en \( x=0 \):

$$ f''(0)=2 \ge 0 $$

Como la segunda derivada es positiva, la función presenta un mínimo local en \( x=0 \).

Demostración

Sea una función definida y continua en un intervalo (a, b).

Si en un punto \( x₀ \in (a, b) \) se cumple que la primera derivada se anula:

$$ f'(x_0)=0 $$

Entonces, de acuerdo con el teorema de Fermat, la función \( f(x) \) puede presentar en \( x₀ \) un mínimo o un máximo local.

Nota. El hecho de que la derivada se anule no garantiza la existencia de un extremo: también podría tratarse de un punto de inflexión.

Si la segunda derivada en \( x₀ \) es positiva:

$$ f''(x_0) > 0 $$

Como la función es continua, el teorema de permanencia del signo asegura que existe un entorno \( (x-\delta,\, x+\delta) \) en el cual \( f''(x) > 0 \).

En ese intervalo la primera derivada \( f'(x) \) resulta creciente y la función \( f(x) \) es convexa.

En una función convexa, la recta tangente en \( x₀ \) se sitúa siempre por debajo de la gráfica de \( f(x) \):

$$ f(x) \ge f(x_0) + f'(x_0)(x - x_0) $$

Y dado que \( f'(x_0)=0 \):

$$ f(x) \ge f(x_0) $$

Esto demuestra que \( x₀ \) es un punto de mínimo local.

Nota. La demostración para un máximo local es análoga, pero parte de la hipótesis de que la segunda derivada en \( x₀ \) es negativa.

Y así sucesivamente.