Determinación de máximos y mínimos mediante derivadas

Los máximos y mínimos de una función \( f(x) \) pueden estudiarse a través de sus derivadas.

Si la primera derivada se anula en \( x₀ \): $$ f'(x_0) = 0 $$ entonces la función presenta:
• un máximo local si la segunda derivada es negativa: $$ f″(x_0) < 0 $$
• un mínimo local si la segunda derivada es positiva: $$ f″(x_0) > 0 $$

Criterio general

El procedimiento para identificar máximos y mínimos puede extenderse de la siguiente manera:

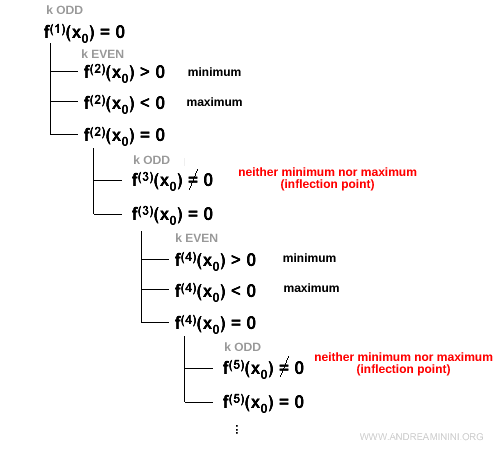
Si la derivada de orden \( k \) se anula en \( x₀ \) y \( k \) es impar:

$$ f^{(k)}(x_0) = 0 \quad \text{con } k \text{ impar} $$

Entonces:

• hay un máximo local si la derivada de orden \( k+1 \) es negativa: $$ f^{(k+1)}(x_0) < 0 $$
• hay un mínimo local si la derivada de orden \( k+1 \) es positiva: $$ f^{(k+1)}(x_0) > 0 $$
• no existe máximo ni mínimo si la derivada de orden \( k+1 \) es cero y la de orden \( k+2 \) es distinta de cero: $$ f^{(k+1)}(x_0) = 0 \quad \text{y} \quad f^{(k+2)}(x_0) \ne 0 $$. En tal caso, la función presenta un punto de inflexión en \( x₀ \).

Nota. Si la derivada de orden \( k \) se anula y \( k \) es par, la función no tiene ni máximo ni mínimo en \( x₀ \) siempre que la derivada de orden \( k+1 \) sea distinta de cero. En esa situación, el punto es de inflexión.

Demostración

Para justificar este criterio partimos del desarrollo en serie de Taylor de una función continua y derivable hasta orden \( n \) en \( x₀ \):

$$ f(x) = \sum_{k=0}^{n} \frac{f^{(k)}(x_0)}{k!} \cdot (x - x_0)^k + R_n(x) $$

De manera explícita:

$$ f(x) = f(x_0) + f^{(1)}(x_0) \cdot \frac{(x - x_0)}{1!} + f^{(2)}(x_0) \cdot \frac{(x - x_0)^2}{2!} + \ldots + f^{(n)}(x_0) \cdot \frac{(x - x_0)^n}{n!} + R_n $$

Supongamos que todas las derivadas hasta el orden \( n-1 \) se anulan en \( x₀ \):

$$ f'(x_0) = f″(x_0) = f^{(3)}(x_0) = \ldots = f^{(n-1)}(x_0) = 0 $$

Entonces, la serie de Taylor se reduce a:

$$ f(x) = f(x_0) + f^{(n)}(x_0) \cdot \frac{(x - x_0)^n}{n!} + R_n $$

Si además la derivada de orden \( n \) en \( x₀ \) es positiva:

$$ f^{(n)}(x_0) > 0 $$

esto indica la presencia de un mínimo local en \( x₀.

Nota. De forma análoga, si \( f^{(n)}(x_0) < 0 \), el punto corresponde a un máximo local.

Consideremos ahora el límite:

$$ \lim_{x \rightarrow x_0} \frac{f(x) - f(x_0)}{(x - x_0)^n} $$

Sustituyendo el desarrollo de Taylor obtenemos:

$$ \lim_{x \rightarrow x_0} \frac{\left[ f(x_0) + f^{(n)}(x_0) \cdot \frac{(x - x_0)^n}{n!} + R_n \right] - f(x_0)}{(x - x_0)^n} $$

lo cual se simplifica en:

$$ \lim_{x \rightarrow x_0} \frac{f^{(n)}(x_0)}{n!} + \lim_{x \rightarrow x_0} \frac{R_n}{(x - x_0)^n} = \frac{f^{(n)}(x_0)}{n!} > 0 $$

Por tanto, el límite es positivo:

$$ \lim_{x \rightarrow x_0} \frac{f(x) - f(x_0)}{(x - x_0)^n} > 0 $$

Distinguimos dos casos según la paridad de \( n \):

• Si \( n \) es par, el denominador \((x - x₀)^n\) es siempre positivo. En consecuencia, \( f(x) > f(x_0) \) en algún entorno \( (x_0 - \delta,\, x_0 + \delta) \). Así, \( x_0 \) es un mínimo local.
• Si \( n \) es impar, el denominador \((x - x₀)^n\) cambia de signo a ambos lados de \( x_0 \), lo que impide que el punto sea un mínimo local.

En conclusión, \( x_0 \) es un mínimo si y solo si \( f^{(n)}(x_0) \ne 0 \) y \( n \) es par.

Ejemplos prácticos

Ejemplo 1 (n par)

Consideremos la función:

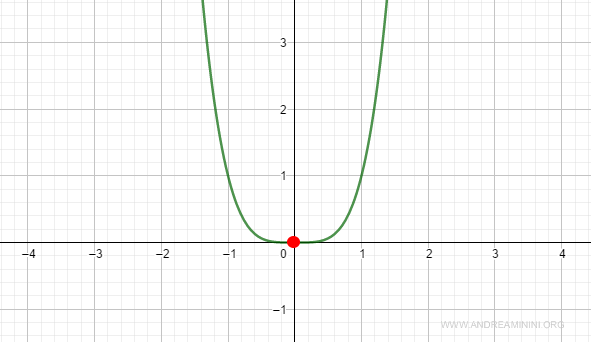
$$ f(x) = x^4 $$

En el punto \( x₀=0 \), la primera, segunda y tercera derivada se anulan:

$$ f^{(1)}(x_0) = 4x^3 = 4(0)^3 = 0 $$

$$ f^{(2)}(x_0) = 12x^2 = 12(0)^2 = 0 $$

$$ f^{(3)}(x_0) = 24x = 24(0) = 0 $$

La cuarta derivada, de orden par, resulta positiva en \( x_0 \):

$$ f^{(4)}(x_0) = 24 > 0 $$

Por lo tanto, la función presenta un mínimo local en \( x_0 \).

Ejemplo 2 (n impar)

Consideremos ahora la función:

$$ f(x) = x^3 $$

En \( x=0 \), tanto la primera como la segunda derivada se anulan:

$$ f^{(1)}(x_0) = 3x^2 = 3(0)^2 = 0 $$

$$ f^{(2)}(x_0) = 6x = 6(0) = 0 $$

No obstante, la tercera derivada, de orden impar, es positiva:

$$ f^{(3)}(x_0) = 6 > 0 $$

En este caso, el punto no corresponde a un mínimo.

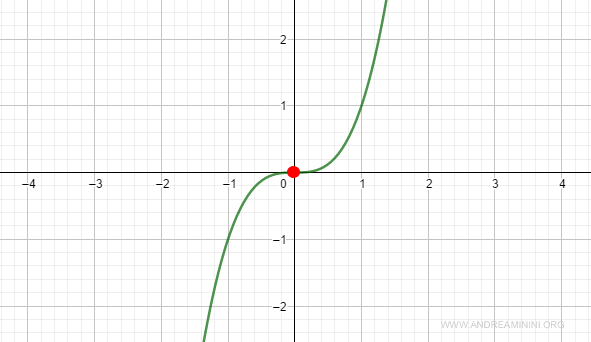
Así, en \( x₀ \) la función tiene un punto de inflexión.

Y así sucesivamente.