Interpretación geométrica de la derivada

Desde una perspectiva geométrica, la derivada de una función expresa la pendiente de su gráfica en un punto x₀; es decir, el gradiente de la recta tangente en x₀.

La ecuación de la recta tangente a la curva en el punto (x₀, f(x₀)) es:

$$ y = f(x_0) + f'(x_0) \cdot (x - x_0) $$

Demostración

Supongamos que la función f(x) está definida en un entorno de x₀.

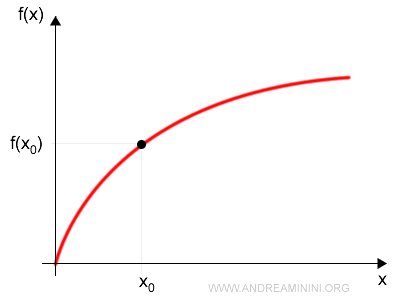
La ecuación de una recta que pasa por x₀ puede escribirse así:

$$ f(x_0) = m x_0 + q $$

Nota. Las variables m y q son desconocidas. Esta ecuación, por lo tanto, representa un número infinito de rectas que atraviesan el punto x₀, formando lo que se denomina un haz de rectas con centro en dicho punto. Entre todas ellas se encuentra la tangente única en x₀.

A continuación, consideremos otro punto x dentro del dominio de la función.

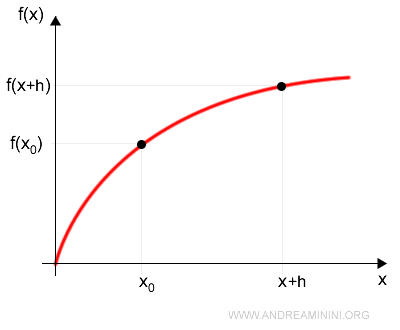
La ecuación de una recta que pasa por x es:

$$ f(x_0 + h) = m (x_0 + h) + q $$

Nota. Nuevamente, m y q son incógnitas. Esta ecuación describe todas las rectas que pasan por el punto x, generando otro haz de rectas con centro en él.

De esta manera, la recta secante que une los puntos x₀ y x se obtiene resolviendo el siguiente sistema de ecuaciones:

$$ \begin{cases} f(x_0) = m x_0 + q \\ f(x_0 + h) = m (x_0 + h) + q \end{cases} $$

Resolviendo este sistema para m y q, primero se determina m y luego q.

Así se llega a la ecuación de la recta secante que pasa por x₀ y x:

$$ y = f(x_0) + \frac{f(x_0 + h) - f(x_0)}{h} \, (x - x_0) $$

Nota. Los pasos algebraicos son los siguientes: $$ \begin{cases} f(x_0) = m x_0 + q \\ f(x_0 + h) = m (x_0 + h) + q \end{cases} $$ $$ \begin{cases} q = f(x_0) - m x_0 \\ f(x_0 + h) = m (x_0 + h) + \bigl(f(x_0) - m x_0\bigr) \end{cases} $$ $$ \begin{cases} q = f(x_0) - m x_0 \\ f(x_0 + h) = m x_0 + m h + f(x_0) - m x_0 \end{cases} $$ $$ \begin{cases} q = f(x_0) - m x_0 \\ \frac{f(x_0 + h) - f(x_0)}{h} = m \end{cases} $$ $$ \begin{cases} q = f(x_0) - \left(\frac{f(x_0 + h) - f(x_0)}{h}\right) x_0 \\ m = \frac{f(x_0 + h) - f(x_0)}{h} \end{cases} $$ De este modo hemos hallado los valores de m y q para la secante: y = m x + q $$ y = m x + q $$ $$ y = \frac{f(x_0 + h) - f(x_0)}{h} \, x + f(x_0) - \left(\frac{f(x_0 + h) - f(x_0)}{h}\right) x_0 $$ $$ y = \frac{f(x_0 + h) - f(x_0)}{h} (x - x_0) + f(x_0) $$

Gráficamente, la secante se representa así:

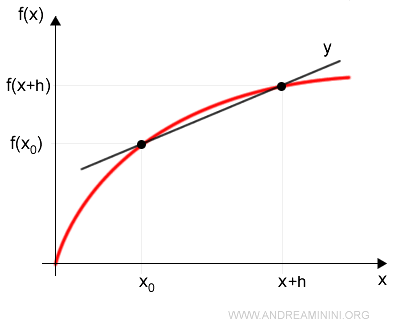
Para obtener la ecuación de la tangente en x₀, se calcula el límite de la secante cuando h tiende a cero:

$$ y_t = \lim_{h \rightarrow 0} \left[ f(x_0) + \frac{f(x_0 + h) - f(x_0)}{h} \, (x - x_0) \right] $$

$$ y_t = f(x_0) + \lim_{h \rightarrow 0} \frac{f(x_0 + h) - f(x_0)}{h} \, (x - x_0) $$

$$ y_t = f(x_0) + f'(x_0) \cdot (x - x_0) $$

Esto confirma que la pendiente de la tangente coincide con la derivada de la función f'(x) evaluada en x₀.

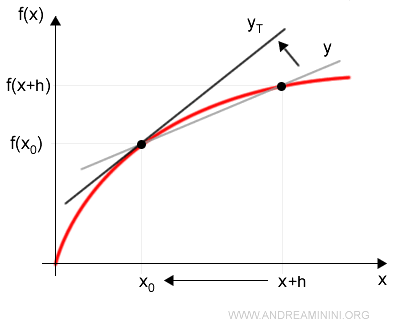
En resumen, la derivada de una función en x₀ determina la pendiente de la tangente en ese punto.

Y así sucesivamente.