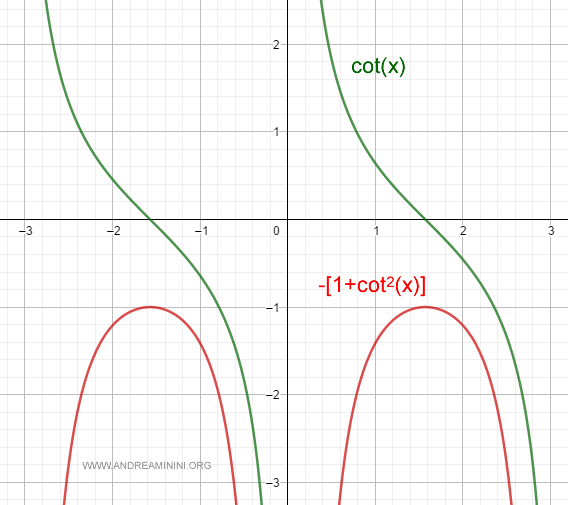
Derivada de la función cotangente

La derivada de la función cotangente es: $$ D[\cot \: x] = \frac{-1}{\sin^2 \: x} = -\bigl(1 + \cot^2 \: x\bigr). $$

Demostración

Para establecer este resultado partimos de la identidad trigonométrica que define la cotangente como el cociente entre coseno y seno:

$$ \cot \: x = \frac{\cos \: x}{\sin \: x}. $$

Nota. El procedimiento es muy similar al utilizado en la derivada de la tangente.

En consecuencia, derivar la cotangente equivale a aplicar la regla del cociente a la fracción coseno/seno:

$$ D[\cot \: x] = D\left[ \frac{\cos \: x}{\sin \: x} \right]. $$

El cálculo es inmediato, ya que conocemos las derivadas elementales del seno y del coseno:

$$ D[\sin \: x] = \cos \: x $$

$$ D[\cos \: x] = -\sin \: x $$

Aplicando la regla del cociente, se obtiene:

$$ D[\cot \: x] = \frac{D[\cos \: x] \cdot \sin \: x - \cos \: x \cdot D[\sin \: x]}{(\sin \: x)^2}. $$

Al sustituir las derivadas del seno y del coseno, resulta:

$$ = \frac{(-\sin \: x) \cdot \sin \: x - \cos \: x \cdot \cos \: x}{(\sin \: x)^2}. $$

Lo cual se simplifica a:

$$ = \frac{-\sin^2 \: x - \cos^2 \: x}{(\sin \: x)^2}. $$

Extrayendo el signo negativo, tenemos:

$$ = \frac{-\bigl(\sin^2 \: x + \cos^2 \: x\bigr)}{(\sin \: x)^2}. $$

Por la identidad pitagórica fundamental sabemos que: $$ \sin^2 \: x + \cos^2 \: x = 1. $$

De este modo, la expresión se reduce a:

$$ \frac{-\bigl(\sin^2 \: x + \cos^2 \: x\bigr)}{(\sin \: x)^2} = \frac{-1}{\sin^2 \: x}. $$

Además, según una identidad trigonométrica que relaciona seno y cotangente: $$ \sin \: x = \frac{1}{\sqrt{1 + \cot^2 \: x}}. $$

Al sustituir esta identidad, obtenemos:

$$ \frac{-1}{\sin^2 \: x} = \frac{-1}{\left(\frac{1}{\sqrt{1 + \cot^2 \: x}}\right)^2} = \frac{-1}{\tfrac{1}{1 + \cot^2 \: x}} = -\bigl(1 + \cot^2 \: x\bigr). $$

Con ello queda plenamente demostrada la fórmula de la derivada de la cotangente.