Derivada de una función lineal
Definición
La derivada de una función lineal f(x)=mx+n es simplemente el coeficiente constante m. $$ f(x)=mx+n \:\: \rightarrow \:\: f'(x)=m $$
Se trata de un resultado inmediato y fácil de verificar.
Demostración
Sea f(x) una función lineal definida en el intervalo (a, b), y x un punto cualquiera de su dominio:
$$ f(x) = mx + n $$
Para calcular la derivada f'(x), aplicamos la definición formal como límite del cociente incremental cuando h tiende a cero:
$$ f'(x) = \lim_{h \rightarrow 0} \frac{f(x+h) - f(x)}{h} $$
Sustituyendo:
- f(x) = mx + n
- f(x+h) = m(x+h) + n
Obtenemos:
$$ \lim_{h \rightarrow 0} \frac{m(x+h) + n - \big(mx + n\big)}{h} $$
$$ \lim_{h \rightarrow 0} \frac{mx + mh + n - mx - n}{h} $$
$$ \lim_{h \rightarrow 0} \frac{mh}{h} $$
$$ \lim_{h \rightarrow 0} m = m $$
Así se confirma que la derivada de una función lineal coincide con su pendiente m.
Ejemplo práctico
Consideremos la siguiente función lineal:
$$ f(x) = 4x + 2 $$
Su gráfica es la siguiente:
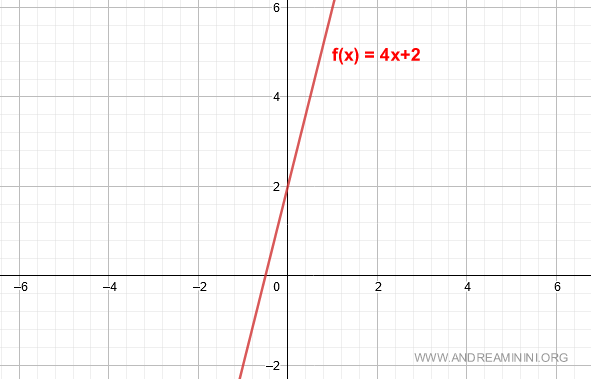
Calculemos la derivada de f(x) utilizando la definición del límite en un punto arbitrario x:
$$ f'(x)= \lim_{h \rightarrow 0} \frac{f(x+h) - f(x)}{h} $$
Como:
- f(x) = 4x + 2
- f(x+h) = 4(x+h) + 2
Al sustituir en el cociente incremental se obtiene:
$$ f'(x)= \lim_{h \rightarrow 0} \frac{4(x+h)+2 - \big(4x+2\big)}{h} $$
$$ f'(x)= \lim_{h \rightarrow 0} \frac{4x + 4h + 2 - 4x - 2}{h} $$
$$ f'(x)= \lim_{h \rightarrow 0} \frac{4h}{h} = 4 $$
Por lo tanto:
$$ f'(x)= 4 $$
La derivada de f(x) coincide con el coeficiente m de la función lineal -en este caso, 4.
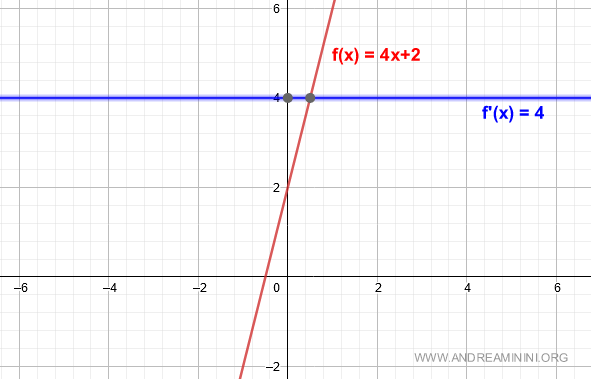
Y así queda demostrado.