Derivada lateral izquierda
Sea una función definida en un intervalo que se extiende hacia la izquierda del punto x0. Decimos que f(x) es diferenciable por la izquierda en x0 si existe el límite lateral izquierdo del cociente incremental entre x y x0, y dicho límite es finito cuando x tiende a x0 desde la izquierda. $$ f'_-(x_0) = \lim_{x \rightarrow x_0^-} \frac{f(x)-f(x_0)}{x - x_0} $$ Como Δx = x − x0, también puede expresarse así: $$ f'_-(x_0) = \lim_{Δx \rightarrow 0^-} \frac{f(x_0 + Δx) - f(x_0)}{Δx} $$ A esta expresión se le denomina derivada lateral izquierda de f(x).
En este contexto, nos interesan únicamente los valores de x situados a la izquierda de x0.
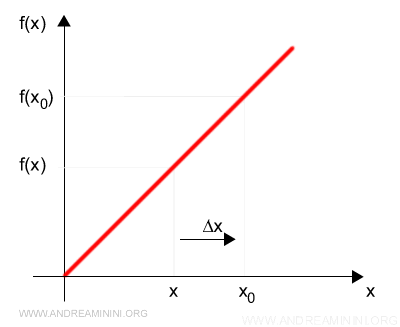
Al calcular la derivada lateral izquierda, la diferencia Δx = x − x0 es siempre negativa.
$$ x - x_0 < 0 $$
Por lo tanto,
$$ Δx < 0 $$
Nota. La notación puede variar según el autor. En ocasiones se escribe el punto x como x0 − δ. No obstante, la idea es exactamente la misma: se trata de un punto inmediatamente a la izquierda de x0 que se aproxima indefinidamente a x0 cuando tomamos el límite.
El intervalo situado a la derecha de x0 no se considera en este caso.
Un ejemplo práctico
Verifiquemos si existe la derivada lateral izquierda de la función f(x) = |x| en el punto x0 = 2.
$$ f(x) = 2 $$
Calculamos el límite cuando x tiende a x0 desde la izquierda:
$$ f'_-(x_0) = \lim_{x \rightarrow x_0^-} \frac{f(x) - f(x_0)}{x - x_0} $$
Sustituyendo x0 = 2, obtenemos:
$$ f'_-(2) = \lim_{x \rightarrow 2^-} \frac{f(x) - f(2)}{x - 2} $$
$$ f'_-(2) = \lim_{x \rightarrow 2^-} \frac{|x| - |2|}{x - 2} $$
$$ f'_-(2) = \lim_{x \rightarrow 2^-} \frac{x - 2}{x - 2} = +1 $$
En este caso, x se aproxima a 2 desde la izquierda sin llegar a alcanzarlo, por ejemplo con valores como 1.999999.
$$ f'_-(2) = \lim_{x \rightarrow 2^-} \frac{x - 2}{x - 2} = \lim_{x \rightarrow 2^-} \frac{1.99999 - 2}{1.99999 - 2} $$
De modo que la diferencia x − 2 es siempre negativa, tanto en el numerador como en el denominador.
$$ f'_-(2) = \lim_{x \rightarrow 2^-} \frac{1.99999 - 2}{1.99999 - 2} = \lim_{x \rightarrow 2^-} \frac{-0.000001}{-0.000001} $$
Por consiguiente, el cociente resulta siempre positivo.
Como los valores del numerador y del denominador coinciden, la fracción se simplifica a +1.
$$ f'_-(2) = \lim_{x \rightarrow 2^-} \frac{-0.000001}{-0.000001} = \lim_{x \rightarrow 2^-} 1 = +1 $$
En conclusión, la derivada lateral izquierda de f(x) en x0 = 2 es igual a +1.
$$ f'_-(2) = +1 $$
Nota. Se puede llegar al mismo resultado empleando la forma alternativa del límite lateral izquierdo: $$ f'_-(x_0) = \lim_{Δx \rightarrow 0^-} \frac{f(x_0 + Δx) - f(x_0)}{Δx} $$ $$ f'_-(2) = \lim_{Δx \rightarrow 0^-} \frac{f(2 + Δx) - f(2)}{Δx} $$ $$ f'_-(2) = \lim_{Δx \rightarrow 0^-} \frac{|2 + Δx| - |2|}{Δx} $$ En el límite por la izquierda, el incremento Δx = x − x0 es siempre negativo, es decir, Δx < 0. Así, podemos reescribir la expresión como: $$ f'_-(2) = \lim_{Δx \rightarrow 0^-} \frac{|2 − Δx| − |2|}{− Δx} $$ La diferencia en el numerador, |2 − Δx| − |2|, resulta siempre negativa. Por tanto, tanto el numerador como el denominador son negativos, lo que hace que el cociente sea positivo. $$ f'_-(2) = \lim_{Δx \rightarrow 0^-} \frac{- Δx}{- Δx} = \lim_{Δx \rightarrow 0^-} 1 = +1 $$ El resultado coincide en ambos planteamientos.
Así es como se obtiene el resultado.