Derivada de la Función Seno
La derivada de la función seno es la función coseno. $$ D[\sin x] = \cos x $$
Demostración
Para demostrar esta regla fundamental de la derivación, partimos de la función seno:
$$ f(x) = \sin x $$
Aplicamos la definición de derivada como límite:
$$ \lim_{h \rightarrow 0} \frac{f(x+h) - f(x)}{h} $$
donde:
$$ f(x) = \sin x $$
$$ f(x+h) = \sin (x + h) $$
Sustituyendo en el cociente incremental:
$$ \lim_{h \rightarrow 0} \frac{\sin (x + h) - \sin (x)}{h} $$
Usamos la identidad trigonométrica: $$ \sin a - \sin b = 2 \cdot \sin \left(\frac{a - b}{2}\right) \cdot \cos \left(\frac{a + b}{2}\right) $$
El numerador se transforma en:
$$ \lim_{h \rightarrow 0} \frac{2 \cdot \sin \left(\frac{h}{2}\right) \cdot \cos \left(x + \frac{h}{2}\right)}{h} $$
Reordenando la expresión:
$$ \lim_{h \rightarrow 0} \frac{\sin \left(\frac{h}{2}\right) \cdot \cos \left(x + \frac{h}{2}\right)}{\tfrac{h}{2}} $$
Esto permite separar el límite en dos factores:
$$ \lim_{h \rightarrow 0} \frac{\sin \left(\tfrac{h}{2}\right)}{\tfrac{h}{2}} \cdot \lim_{h \rightarrow 0} \cos \left(x + \tfrac{h}{2}\right) $$
El primer límite es un resultado clásico:
$$ \lim_{t \rightarrow 0} \frac{\sin t}{t} = 1 $$
La expresión queda reducida a:
$$ 1 \cdot \lim_{h \rightarrow 0} \cos \left(x + \tfrac{h}{2}\right) $$
Cuando \( h \) tiende a cero, este límite vale \(\cos x\):
$$ 1 \cdot \cos x $$
En conclusión, la derivada de \(\sin(x)\) es:
$$ f'(x) = \cos x $$
Hemos establecido, por tanto, que la derivada de la función seno es la función coseno.
Representación gráfica
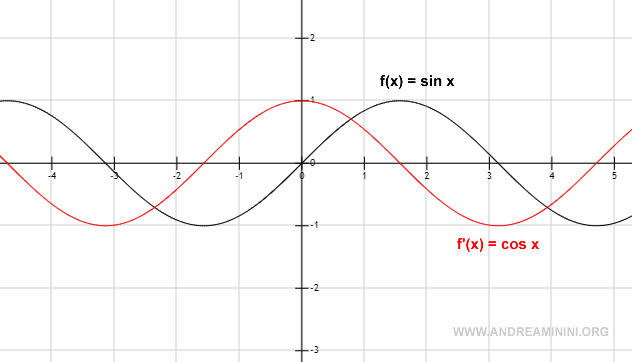
Un Ejemplo Práctico
Veamos el siguiente caso:
$$ f(x) = \sin (x^2) $$
Nota: Cuando el argumento del seno no es simplemente \( x \), no podemos aplicar de manera directa la regla básica. Se trata de una función compuesta del tipo \( f(g(x)) \), y por ello la derivada no es simplemente \(\cos(x^2)\).
Estamos, pues, ante un caso típico de función compuesta, donde es necesario aplicar la regla de la cadena:
$$ f'(x) = f'(g(x)) \cdot g'(x) $$
En este ejemplo:
$$ f'(g(x)) = D[\sin(g(x))] = \cos(x^2) $$
$$ g'(x) = D[x^2] = 2x $$
Al sustituir en la regla de la cadena obtenemos:
$$ f'(x) = \cos(x^2) \cdot 2x $$
De modo que la derivada de \(\sin(x^2)\) es:
$$ f'(x) = 2x \cdot \cos(x^2) $$
Representación gráfica
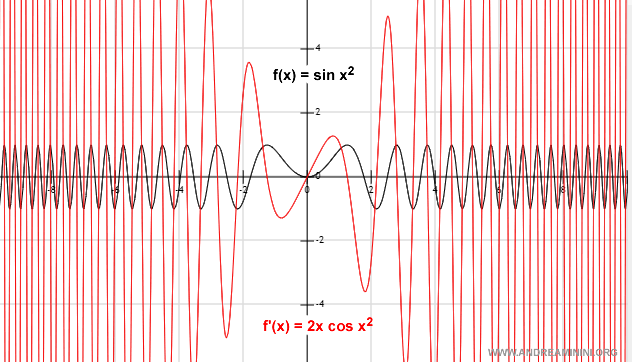
Y con esto queda demostrado.