Derivada de un vector unitario
¿Qué entendemos por la derivada de un vector unitario?
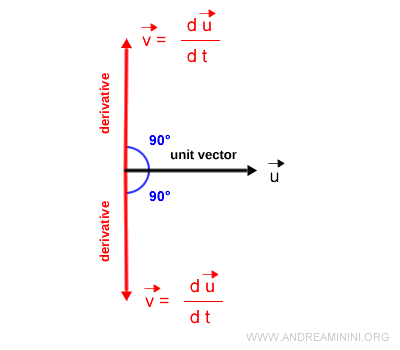
La derivada de un vector unitario (u) es siempre un vector (v) perpendicular al propio vector. $$ \frac{d \vec{u}}{dt} = \vec{v} \ \ \ donde \ \ \ \vec{v} \perp \vec{u} $$
En otras palabras, para cualquier vector unitario u, su derivada es un vector ortogonal a u, es decir, forma un ángulo recto con él.
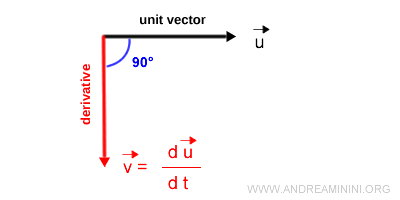
La derivada del vector unitario se encuentra sobre la dirección normal a u y puede apuntar en cualquiera de los dos sentidos posibles de esa normal.
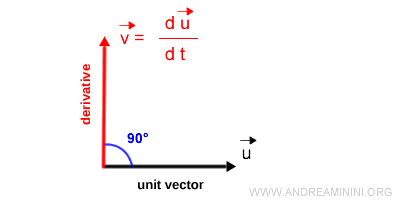
Nota. En la demostración que sigue se detallan todos los pasos que justifican este resultado. Para comprenderla plenamente conviene estar familiarizado con el producto escalar.
Demostración
Partamos de un vector unitario arbitrario:
$$ \vec{u} $$
Un vector unitario es, por definición, un vector cuya magnitud es igual a uno.
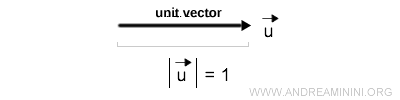
Nota. Un vector unitario puede orientarse en cualquier dirección. En esta demostración, por simplicidad, lo consideramos paralelo al eje x para facilitar la visualización.
Calculemos el producto escalar de u consigo mismo:
$$ \vec{u} \cdot \vec{u} = |u| \cdot |u| \cdot \cos \alpha $$
Aquí |u| es la magnitud del vector y α el ángulo entre ambos vectores en el producto escalar.
Como se trata del mismo vector, el ángulo es α = 0:
$$ \vec{u} \cdot \vec{u} = |u| \cdot |u| \cdot \cos 0 $$
Sabemos que cos(0) = 1:
$$ \vec{u} \cdot \vec{u} = |u| \cdot |u| $$
Y dado que u es unitario, |u| = 1:
$$ \vec{u} \cdot \vec{u} = 1 $$
Diferenciemos ahora este producto respecto al tiempo:
$$ \frac{d (\vec{u} \cdot \vec{u}) }{dt} $$
Como el producto escalar es 1, su derivada es la derivada de una constante, es decir, cero:
$$ \frac{d (\vec{u} \cdot \vec{u}) }{dt} = \frac{d (1) }{dt} = 0 $$
Pero también podemos aplicar la regla del producto a la derivada del producto escalar:
$$ \frac{d (\vec{u} \cdot \vec{u}) }{dt} = \frac{d \vec{u} }{dt} \cdot \vec{u} + \vec{u} \cdot \frac{d \vec{u}}{dt} $$
Ambos resultados deben coincidir con d(1)/dt = 0, de modo que:
$$ \frac{d \vec{u} }{dt} \cdot \vec{u} + \vec{u} \cdot \frac{d \vec{u}}{dt} = 0 $$
Los dos términos son iguales, por lo que se pueden agrupar:
$$ 2 \left( \frac{d \vec{u} }{dt} \cdot \vec{u} \right) = 0 $$
El factor 2 es positivo, de modo que necesariamente:
$$ \frac{d \vec{u} }{dt} \cdot \vec{u} = 0 $$
Esto significa que el producto escalar entre la derivada de u y el propio vector es nulo.
Un producto escalar igual a cero indica que los vectores son ortogonales, es decir, forman un ángulo recto.
Por tanto, la derivada de un vector unitario es perpendicular al propio vector:
$$ \frac{d \vec{u} }{dt} \perp \vec{u} $$
En otras palabras, la derivada de un vector unitario se encuentra sobre la dirección normal a u.
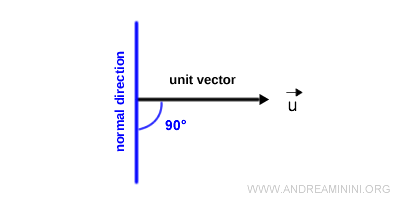
Puede apuntar tanto hacia la normal exterior como hacia la interior.
Y así sucesivamente.