Teorema de Rolle

Si una función \( f(x) \) es continua en [a,b], derivable en (a,b) y cumple que \( f(a) = f(b) \), entonces existe al menos un punto \( x_0 \in (a,b) \) tal que su primera derivada se anula: $$ f'(x_0)=0 $$

Demostración

Sea \( f(x) \) una función continua en [a,b] y derivable en (a,b). Por el teorema de los valores extremos, una función continua en un intervalo cerrado alcanza necesariamente un mínimo (en \( x_1 \)) y un máximo (en \( x_2 \)) dentro de ese intervalo.

$$ f(x_1) \le f(x) \le f(x_2) $$

Para probar que existe al menos un punto donde la derivada es cero, distinguimos dos casos:

1) El mínimo o el máximo se encuentra en el interior del intervalo

Si al menos uno de los valores extremos -ya sea el máximo en \( x_2 \) o el mínimo en \( x_1 \)- se alcanza en un punto estrictamente interior de (a,b), entonces, según el teorema de Fermat, la derivada en ese punto debe anularse.

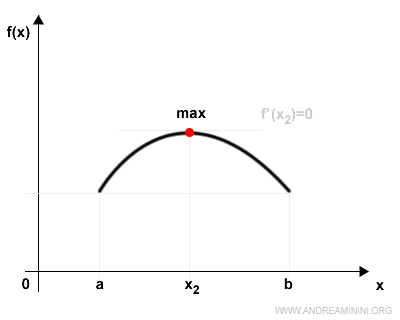
En este caso, existe al menos un punto \( x \in (a,b) \) tal que \( f'(x) = 0 \).

2) El mínimo y el máximo se alcanzan en los extremos

Si tanto el mínimo (\( x_1 \)) como el máximo (\( x_2 \)) corresponden a los extremos del intervalo, es decir, no hay extremos en el interior, entonces:

$$ f(x_1) = f(a) \\ f(x_2) = f(b) $$

Y como, por hipótesis, \( f(a) = f(b) \), se tiene:

$$ f(x_1) = f(x_2) $$

Esto significa que el valor mínimo y el máximo coinciden, y por lo tanto la función debe permanecer constante en todo el intervalo (a,b):

$$ f(x_1) \le f(x) \le f(x_2) $$

$$ f(x_1) = f(x) = f(x_2) $$

Si \( f(x) \) es constante para todo \( x \in (a,b) \), entonces su derivada se anula en cada punto del intervalo.

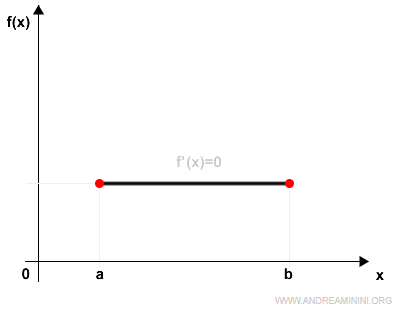
En esta situación, existen infinitos puntos de (a,b) en los que la derivada \( f'(x) \) es igual a cero.

Con ello queda demostrado el teorema de Rolle: si \( f(a) = f(b) \), entonces debe existir al menos un punto en el intervalo abierto (a,b) donde \( f'(x) = 0 \).

Y así sucesivamente.