Derivada de la función arcoseno
La derivada de la función arcoseno es: $$ D[\arccos x] = \frac{-1}{\sqrt{1 - x^2}}. $$
Este resultado se obtiene aplicando la regla general de derivación de funciones inversas.
Nota. En trigonometría, el arcoseno es la función inversa del coseno en el intervalo $(0, \pi)$.
La función arcoseno y su interpretación
La función coseno no es monótona en todo su dominio real:
$$ f(x) = \cos x $$
No obstante, al restringirla al intervalo cerrado $[0, \pi]$, se vuelve monótona estrictamente decreciente, y sus valores oscilan entre $1$ y $-1$.
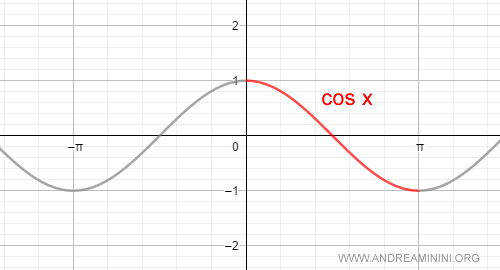
Al ser continua y monótona en $[0, \pi]$, la función coseno resulta también invertible en dicho intervalo.
Su inversa es la función arcoseno:
$$ f^{-1}(x) = \arccos x $$
¿Por qué se llama arcoseno? Se denomina así porque determina la longitud del arco -es decir, el ángulo en grados o radianes sobre la circunferencia unitaria- que corresponde a un valor dado del coseno.
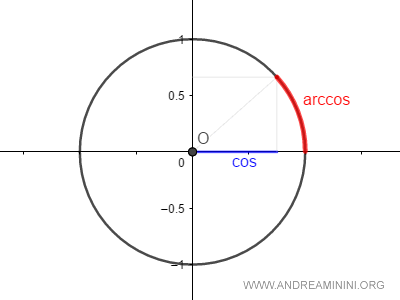
Como el coseno y el arcoseno son funciones inversas: $$ y = \cos x \\ x = \arccos y $$ Por tanto: $$ y = \cos(\arccos y) \\ x = \arccos(\cos x) $$
El dominio de la función arcoseno es el intervalo cerrado $[-1, 1]$.
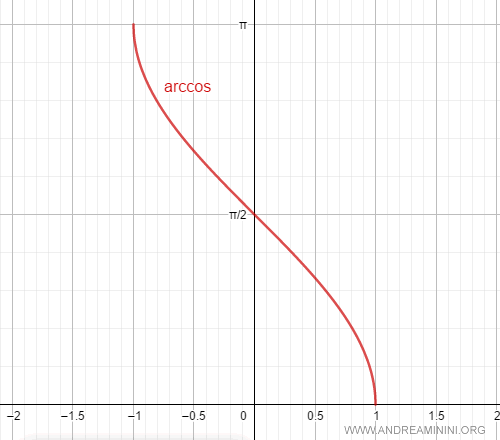
En consecuencia, la función arcoseno es derivable en el intervalo abierto $(-1, 1)$.
Demostración y desarrollo
La función arcoseno se define como la inversa de la función coseno:
$$ f^{-1}(f(y)) = \arccos x $$
donde $f(y)$ está dada por:
$$ f(y) = \cos y $$
Para derivar la función arcoseno aplicamos la regla de la derivada de la función inversa:
$$ D[f^{-1}] = \frac{1}{D[f(y)]}. $$
De ahí se deduce:
$$ D[\arccos x] = \frac{1}{D[\cos y]}. $$
Como la derivada del coseno es $-\sin y$, resulta:
$$ D[\arccos x] = \frac{1}{- \sin y}. $$
Nota. Recordemos la identidad trigonométrica: $$ \sin y = \sqrt{1 - \cos^2 y}. $$
Sustituyendo en la expresión obtenemos:
$$ D[\arccos x] = \frac{1}{- \sqrt{1 - \cos^2 y}}. $$
Que se simplifica en:
$$ D[\arccos x] = - \frac{1}{\sqrt{1 - \cos^2 y}}. $$
Nota. Como $$ y = \arccos x, $$ se sigue que $$ \cos y = \cos(\arccos x) = x. $$ En consecuencia, podemos sustituir: $$ \cos^2 y = \cos^2(\arccos x) = x^2. $$
Así llegamos finalmente a:
$$ D[\arccos x] = - \frac{1}{\sqrt{1 - x^2}}. $$
Con esto queda establecida la fórmula de la derivada de la función arcoseno.
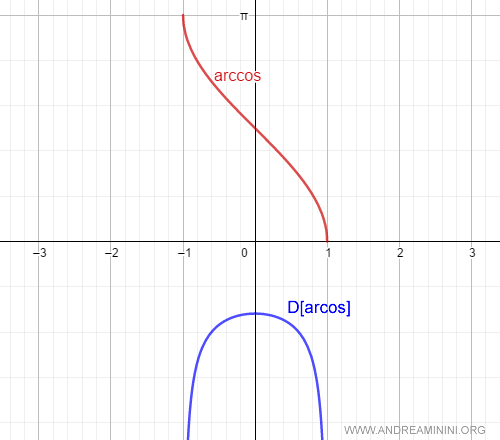
Y a partir de aquí pueden desarrollarse otros resultados.