Derivada del valor absoluto

Definición

La derivada de la función valor absoluto |x| es la función signo: $$ D[ \: |x| \: ] = \frac{x}{|x|} = \frac{|x|}{x} $$

La función signo puede escribirse con |x| en el numerador o en el denominador.

Ambas expresiones conducen al mismo resultado.

Demostración

La función valor absoluto

$$ f(x)=|x| $$

puede expresarse de forma equivalente como

$$ f(x)=\sqrt{x^2} $$

Nota. El valor absoluto de una variable |x| equivale a la raíz cuadrada de su cuadrado.

Como la derivada de una raíz cuadrada es

$$ D[\sqrt{x}]=\frac{1}{2 \sqrt{x}} $$

aplicamos esta regla a f(x):

$$ D[\sqrt{x^2}]=\frac{2x}{2 \sqrt{x^2}}= \frac{x}{\sqrt{x^2}}$$

De este modo obtenemos la derivada de f(x):

$$ f'(x) = \frac{x}{\sqrt{x^2}}$$

Y como la raíz cuadrada de \( x^2 \) es simplemente |x|, podemos reescribir f'(x) como:

$$ f'(x) = \frac{x}{|x|}$$

Así llegamos a la derivada de |x|, que corresponde a la función signo, también denominada sgn(x).

 

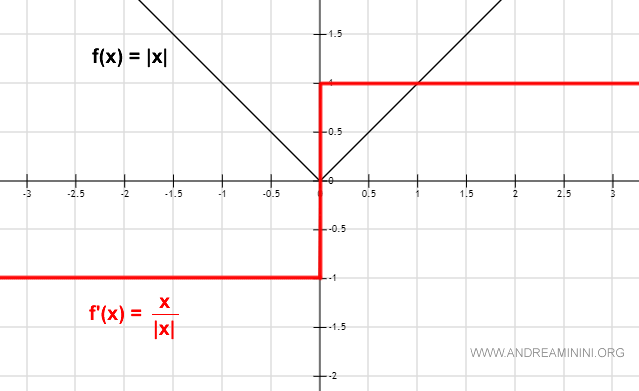
La función signo toma el valor 1 cuando \( x \) es positivo (x > 0) y -1 cuando \( x \) es negativo (x < 0).

Nota. La función signo no es derivable en x = 0.

Método alternativo

También es posible demostrar la derivada de la función valor absoluto de otra manera.

Podemos expresar \( f(x) = |x| \) como una función a trozos:

$$ f(x) = \begin{cases} f(x)=x \:\: \text{si} \:\: x \gt 0 \\ f(x)=-x \:\: \text{si} \:\: x \lt 0 \end{cases} $$

Derivando cada tramo por separado obtenemos:

$$ f'(x) = \begin{cases} f'(x)=1 \:\: \text{si} \:\: x \gt 0 \\ f'(x)=-1 \:\: \text{si} \:\: x \lt 0 \end{cases} $$

Esto nos lleva al mismo resultado: la derivada es la función signo:

$$ f'(x) = sgn \: x $$

Y con esto queda demostrado.