Derivada de la función arcotangente
La derivada de la función arcotangente es: $$ D[\arctan x] = \frac{1}{1 + x^2}. $$
Este resultado se obtiene a partir de que la función arcotangente es la inversa de la tangente.
Por ello, podemos aplicar directamente la regla de derivación de funciones inversas.
Demostración y explicación
La función tangente es continua, pero no resulta monótona en toda la recta real:
$$ f(x) = \tan x $$
No obstante, restringida al intervalo abierto $(-\pi/2, \pi/2)$, la tangente es estrictamente creciente, y por tanto monótona.
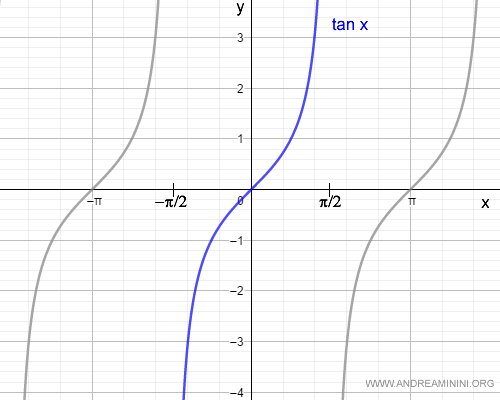
En este intervalo $(-\pi/2, \pi/2)$, la función $\tan x$ es invertible, y su función inversa es la arcotangente:
$$ f^{-1}\bigl(y = \tan x\bigr) = \arctan x $$
¿Qué es la arcotangente? Desde el punto de vista geométrico, la arcotangente representa el ángulo $\alpha$ (en radianes o grados) sobre la circunferencia unitaria que corresponde a un valor dado de la tangente.
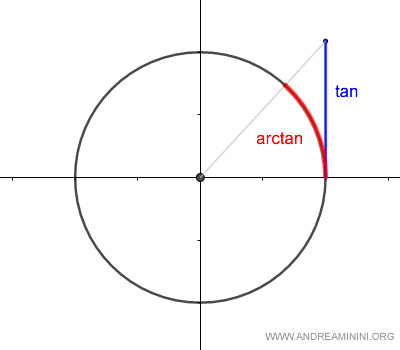
De este modo, tangente y arcotangente son funciones inversas entre sí:
$$ y = \tan \alpha $$ $$ \alpha = \arctan y $$ Por consiguiente: $$ y = \tan(\arctan y) $$ y $$ \alpha = \arctan(\tan \alpha). $$
El dominio de la función arcotangente es toda la recta real $\mathbb{R}$, mientras que su recorrido (codominio) es el intervalo $(-\pi/2, \pi/2)$.
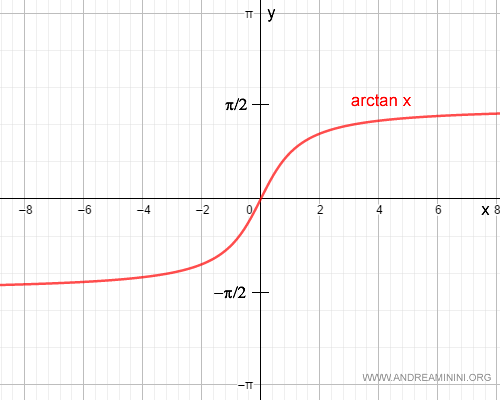
Los límites de la función arcotangente en el infinito positivo y negativo son:
$$ \lim_{x \to +\infty} \arctan x = \frac{\pi}{2} $$
$$ \lim_{x \to -\infty} \arctan x = -\frac{\pi}{2} $$
Por tanto, la función arcotangente es derivable en todo $\mathbb{R}$.
Para calcular su derivada aplicamos la regla de la derivada de la función inversa:
$$ D[f^{-1}(y)] = \frac{1}{D[f(y)]}. $$
De donde se sigue:
$$ D[\arctan x] = \frac{1}{D[\tan y]}. $$
La derivada de la tangente es $1/\cos^2 y$:
$$ D[\arctan x] = \frac{1}{\frac{1}{\cos^2 y}}. $$
Nota. Usando la identidad pitagórica $\cos^2 y + \sin^2 y = 1$, el denominador puede escribirse como $\cos^2 y + \sin^2 y$.
$$ D[\arctan x] = \frac{1}{\frac{\cos^2 y + \sin^2 y}{\cos^2 y}}. $$
$$ D[\arctan x] = \frac{1}{\frac{\cos^2 y}{\cos^2 y} + \frac{\sin^2 y}{\cos^2 y}}. $$
$$ D[\arctan x] = \frac{1}{1 + \frac{\sin^2 y}{\cos^2 y}}. $$
Nota. Como $\tan y = \sin y / \cos y$, al elevar al cuadrado obtenemos $\tan^2 y = \sin^2 y / \cos^2 y$.
$$ D[\arctan x] = \frac{1}{1 + \tan^2 y}. $$
Nota. Como $y = \arctan x$:
$$ D[\arctan x] = \frac{1}{1 + \tan^2(\arctan x)}. $$
Nota. Al ser la tangente y la arcotangente funciones inversas: $$ y = \arctan x \quad \text{y} \quad x = \tan y, $$ se cumple que $$ \tan(\arctan x) = x. $$ Por lo tanto: $$ \tan^2(\arctan x) = x^2. $$
En conclusión:
$$ D[\arctan x] = \frac{1}{1 + x^2}. $$
Con esto queda establecida la fórmula de la derivada de la función arcotangente.
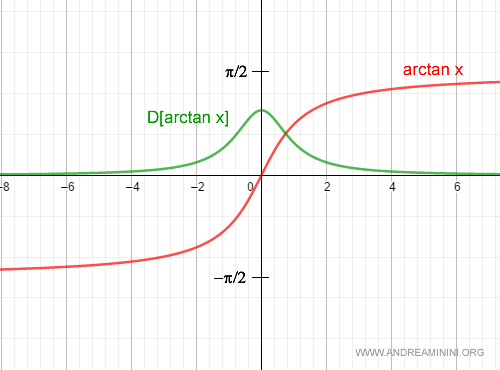
A partir de aquí pueden derivarse otros resultados.