Derivada de la raíz cuadrada
La derivada de una raíz cuadrada es: $$ D[\sqrt{x}] = \frac{1}{2 \cdot \sqrt{x}} $$
Demostración
Vamos a demostrar esta regla partiendo de la función:
$$ f(x) = \sqrt{x} $$
Consideramos el cociente incremental:
$$ \lim_{h \rightarrow 0} \frac{f(x+h)-f(x)}{h} $$
donde
$$ f(x)=\sqrt{x}, \quad f(x+h)=\sqrt{x+h} $$
Sustituyendo en el cociente incremental obtenemos:
$$ \lim_{h \rightarrow 0} \frac{\sqrt{x+h}-\sqrt{x}}{h} $$
Para simplificar el cociente incremental, multiplicamos numerador y denominador por el conjugado:
$$ \lim_{h \rightarrow 0} \frac{\sqrt{x+h}-\sqrt{x}}{h} \cdot \frac{\sqrt{x+h}+\sqrt{x}}{\sqrt{x+h}+\sqrt{x}} $$
Al desarrollar el numerador:
$$ \lim_{h \rightarrow 0} \frac{(\sqrt{x+h})^2 - (\sqrt{x})^2}{h \, (\sqrt{x+h}+\sqrt{x})} $$
lo que se simplifica a:
$$ \lim_{h \rightarrow 0} \frac{(x+h) - x}{h \, (\sqrt{x+h}+\sqrt{x})} $$
$$ \lim_{h \rightarrow 0} \frac{h}{h \, (\sqrt{x+h}+\sqrt{x})} $$
$$ \lim_{h \rightarrow 0} \frac{1}{\sqrt{x+h}+\sqrt{x}} $$
Tomando el límite cuando \( h \to 0 \):
$$ \frac{1}{\sqrt{x}+\sqrt{x}} = \frac{1}{2\sqrt{x}} $$
Así demostramos la derivada de la raíz cuadrada de \( x \).
Representación gráfica
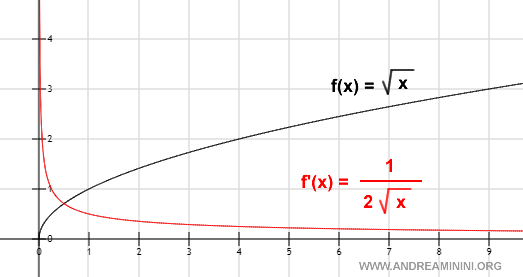
Un ejemplo práctico
Calculemos ahora la derivada de la siguiente función:
$$ f(x) = \sqrt{3x+1} $$
Nota. Al derivar una raíz cuadrada hay que tener cuidado: en muchos casos no basta con aplicar de forma directa la regla básica. Por ejemplo, aquí la derivada NO es:
$$ \frac{1}{2 \sqrt{3x+1}} \:\:\: \text{(incorrecto)} $$ $$ \frac{1}{2 \sqrt{3}} \:\:\: \text{(incorrecto)} $$
En este caso la función es compuesta, \( g[h(x)] \), donde:
$$ g(x) = \sqrt{h(x)}, \quad h(x) = 3x+1 $$
Por tanto, debemos aplicar la regla de la cadena.
La regla de la cadena establece que:
$$ g'[h(x)] \cdot h'(x) $$
Aquí:
$$ g'[h(x)] = D[ \sqrt{h(x)} ] = \frac{1}{2\sqrt{h(x)}} = \frac{1}{2\sqrt{3x+1}} $$
y
$$ h'(x) = D[3x+1] = 3 $$
Multiplicando ambos resultados:
$$ g'[h(x)] \cdot h'(x) = \frac{1}{2\sqrt{3x+1}} \cdot 3 = \frac{3}{2\sqrt{3x+1}} $$
En conclusión, la derivada de \( f(x) \) es:
$$ f'(x) = \frac{3}{2\sqrt{3x+1}} $$
Ese es el resultado final.